[1ereS] DM préparation suite

[Mqtt-95]

Bonjour,

Hier j'avais demander de l'aide pour un DM sur lequel je bloquais pour certaine question, j'ai apprécié l'aide que j'ai eu et réussi à terminer l'exercice en question.

Or, maintenant je bloque sur un autre exercice de ce même DM :/

"1. Soient a et b deux nombres rationnels tels que

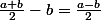
De même pour je n'arrive pas à déterminer le signe :/

Merci d'avance de bien vouloir m'aider

[Mqtt-95]

Je me permet de remonter le sujet, je n'ai toujours pas trouvé, si quelqu'un saurait me guider sur la résolution de l'exercice :/

[Nightmare]

Salut,

1. On te dit que a < b, il ne faut pas l'oublier !

[Mqtt-95]

Ah oui.. Effectivement j'ai réussi à faire la première question, merci =)

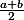
Si quelqu'un saurait m'expliquer la 2e, je dois montrer que est forcément plus petit que 1 ?

[Nightmare]

Salut !

Relis bien la question, on te demande de montrer qu'il n'existe pas de plus petit rationnel supérieur à un. Autrement dit, il faut montrer que quelque soit le rationnel supérieur à un, on va toujours pouvoir en trouver un plus petit. Pas très difficile avec la question 1 !

[Mqtt-95]

Mmh, désolé d'insister mais je ne comprends vraiment pas.

Vu que je dois utiliser un raisonnement par l'absurde, j'admets en hypothèse qu'il existe un plus petit nombre rationnel R supérieur à un. Or je ne comprends même pas cet hypothèse, je n'arrive pas à la mathématisé x)

[Nightmare]

Qu'est-ce que tu ne comprends pas ? Je ne peux pas expliquer plus la proposition que je ne l'ai fait dans mon post précédent.

Qu'as-tu réellement montré en 1? Tu as montré qu'entre deux rationnels, il y a toujours un autre rationnel.

Maintenant on te demande de montrer qu'entre le nombre 1 et un rationnel supérieur à ce dernier, il y a toujours un autre rationnel (es-tu d'accord déjà que c'est ce qu'il faut montrer?)

[Mqtt-95]

Ce que je ne comprends pas c'est "plus petit nombre rationnel supérieur à 1", également le fait qu'il est dit "qu'il n'existe pas".

[Nightmare]

Moi je ne comprends pas ce que tu ne comprends pas, la phrase parle d'elle même. Tu sais ce qu'est un nombre rationnel, tu sais ce que veut dire "être plus petit" et tu sais ce que veut dire "être supérieur à 1" donc à priori tu devrais pouvoir déchiffrer la phrase en faisant un petit effort, surtout que je te l'ai expliquée déjà 2 fois.

Je peux réessayer une 3ème fois :

On est d'accord qu'il existe des nombres rationnels supérieurs à 1 ? 3/2 par exemple, 5/4, etc.
En fait il y en a une infinité (déjà, tous les rationnels de la forme (n+1)/n). L'idée de l'exercice est de montrer que parmi tous ces rationnels supérieurs à 1, il n'y en a pas un qui est plus petit que tous les autres.

[Mqtt-95]

Désolé de répondre si tard, je finissait les autres exercices en attendant =)

Merci de ta patience en tout cas =D J'ai enfin saisi la question et je pense pouvoir y répondre sans difficulté =)