Bonjour, je viens de finir mon année de Terminale S et je vais passer l'année prochaine en prépa ECS (anciennement HEC). J'ai de nombreuses choses à faire durant les vacances, dont un énorme devoir maison à rendre à la rentrée en mathématiques. Il est censé représenter ce qu'on doit avoir acquis en fin de Terminale S, c'est pourquoi je me permets d'écrire ce sujet dans cette section. Mais il y a de nombreuses questions, malgré une longue réflexion et des recherches, que je n'arrive pas à résoudre, et dont je ne comprends pas du tout comment faire pour avancer. Il faut remarquer que je n'ai pas suivi l'enseignement de spécialité maths, ce qui peut éventuellement être une source d'incompréhension pour certaines questions, je ne sais pas. La plupart du temps j'ai des idées et j'arrive à avancer mais pas à terminer, il y a toujours des blocages. Pourriez-vous m'aider s'il vous plait? Merci d'avance.
Exercice I :
I.2.a. Montrer que pour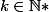 
:
+(\frac{1}{(k+1)^{2}})} = 1+\frac{1}{k(k+1)})
I.2.b. En remarquant que
} = \frac{1}{k}-\frac{1}{k+1})
,
Simplifier :
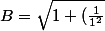+(\frac{1}{2^{2}})} + \sqrt{1+(\frac{1}{2^{2}})+(\frac{1}{3^{2}})} + \sqrt{1+(\frac{1}{3^{2}})+(\frac{1}{4^{2}})} + ... + \sqrt{1+(\frac{1}{2015^{2}})+(\frac{1}{2016^{2}})})
I.6. Simplifier :
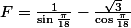I.7. Simplifier :
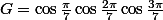
(On pourra multiplier par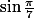 
)I.8. Soit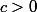 
Pour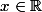 
, on pose  = \frac{x}{\sqrt{1+cx^2}})
Calculer ))
puis )))
Exercice II :
Démontrer que pour tous les réels
,
et
:
II.1.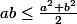 
II.2. Pour et strictement positifs :
 \geq \ln(2)+\frac{1}{2}(\ln a + \ln b))
II.3. Dans le cas où , et non nuls :
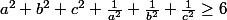
II.4. Pour 
, 
et 
positifs :
(y+z)(x+z))
II.5. Démontrer que, pour tout 
:
 \leq x)
II.6. Sans calculatrice et sans valeurs approchées déterminer quel est le plus grand nombre entre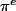 
et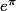 
(On pourra étudier la fonction  = \frac{\ln x}{x})
sur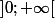 
)Exercice III (je rappelle ne pas avoir fait spé Maths, il y a même un symbole que je connais pas ici) :
III.3. Résoudre :
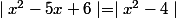
III.4. Résoudre l'équation :
!}+\frac{(x+1)!}{2!(x-1)!} = 14)
où est un entier supérieur à 3 et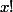 
désigne le produit des facteurs , )
, 
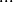, 1
Exemple :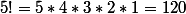 
III.5. Résoudre les systèmes suivants :
\begin{cases} & x^2+2y = -5\\ & 2x^2y = -6 \end{cases})
On pourra poser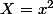 
et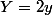 
\begin{cases} & 2x+3y = 7\\ & \ln (x)+2\ln (y) = \ln (2) \end{cases})
J'éditerai mon post pour rajouter les autres questions au fur et à mesure, et je mettrai en rouge les questions auxquelles je n'ai toujours pas réussi à répondre et en vert les questions auxquelles j'aurai réussi à répondre. Merci d'avance.
