J'espère être dans le bon forum, je ne sais pas à quel niveau correspond ma question.
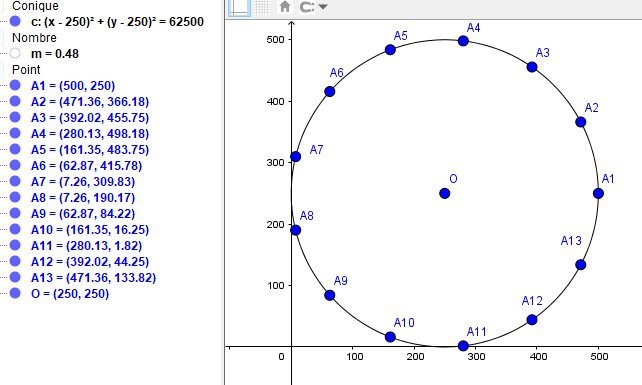
Bref. J'ai donc un cercle, je souhaite placer 13 points à équi-distance les uns des autres, sur ledit cercle.
Je connais le centre, le rayon.
Si (x1,y1) est un point au hasard, par quelle formule je trouve les coordonnées des points suivants sur le cercle ?
J'ai bien essayé de cherché, mais d'après Google c'est impossible à construire
 je m'en moque, c'est l'ordinateur qui le fera, moi il me faut juste la formule pour passer d'un point à un autre
je m'en moque, c'est l'ordinateur qui le fera, moi il me faut juste la formule pour passer d'un point à un autre D'avance merci
Edit : j'ai oublié de préciser qu'il y a bien bien longtemps que j'ai quitté l'école, soyez indulgents et....n'hésitez pas à m'expliquer comme si j'avais 6 ans.
Enfin une formule toute prête m'aiderai plus que des explications






![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)