Petites questions sur la dérivation notamment .

[Trident]

Bonjour à tous, j'ai plusieurs petite questions.

1° Quel est l'ensemble de définition de la fonction qui à x fait correspondre Racine de Sin(x).

Je sais que c'est [ 2kPi ; (2k+1)Pi ] grâce à la correction.

Comment le savoir ça ?

Moi en visualisant le cercle trigonométrique, je constate que c'est [ 0; Pi]

Avez vous une méthode pour savoir ça ? Comment ça se passe dans votre cerveau ? lol.
Passez moi d'autres exemples s'il vous plaît, il faut que je connaisse ça.

2° Est-il possible dans sa calculatrice TI84+ de rentrer la fonction suivante :

f(x) = 2-x² si x<1

f(x) = 1/x si x> (ou =) 1.

Merci.

3° Est-ce que ma démonstration est juste ?

Démontrer que les définitions 1° et 2° sont équivalentes.


Définition 1° .

On dit que f est dérivable en a si et ssi le quotient f(a+h)-f(a) / h admet une limite finie lorsque h tend vers 0. Cette limite est notée f'(a) et est appelée nombre dérivé de f en a. On a donc :

Lim quand h tend vers 0 de f(a+h)-f(a) / h = f'(a) .

Définition n°2 .

On dit que f est dérivable en a si et ssi il existe une fonction E (epsilon) et un réel l tels que :

f(a+h) = f(a) + hl + h fois E(h) avec lim quand h tend vers 0 de E(h) = 0.

Le réel l est le nombre dérivée de f en a, f'(a).


Ma démonstration (pour la moindre faute, alertez moi lol).

Lim quand h tend vers 0 de f(a+h)-f(a) / h = f'(a)
<==> f(a+h)-f(a) / h = f'(a) + E(h) avec lim quand h tend vers 0 de E(h) = 0.

<==> f(a+h) - f(a) = h x ( f'(a) + E(h) )

<==> f(a+h) = hf'(a) + h E(h) + f(a)

<==> f(a+h) = f(a) +hl + h E(h) avec lim quand h tend vers 0 de E(h) = 0 et avec l le nombre dérivée de f en a, f'(a).

CQFD.


Voilà, merci à celui qui répondra à une de ces trois questions .

[Arnaud-29-31]

Salut,

1) Lorsqu'on étudie , on se demande d'abord quand est-ce que sin(x) est défini, réponse : pour tout x.
Ensuite on s'intéresse à la racine, une racine carrée est définie ssi ce qu'il y'a dessous est positif ou nul. Il faut donc que . Si on parcours le cercle trigo, c'est vrai comme tu le dis sur 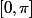ensuite sur ce n'est plus vrai mais cela redevient vrai sur etc ... et au final c'est vrai sur tout intervalle avec p un entier pair. Or un entier pair p peut s'écrire p = 2k avec k n'importe quel entier d'ou l'expression proposée .

2) Rentre les deux fonctions et puis garde les morceaux que tu veux garder.

3) La rédaction peut être améliorée, mais ca me va.

[Trident]

Merci Arnaud, tu voulais dire sin(x) > (ou égale) à 0 pour le 1°. ;)

2° Ouais mais dès fois, les fonctions se rentrent un peu dedans et ça devient pas très lisible, je sais qu'il existe une fonction pour "effacer" la fonction sur la partie ]1;+inf[ et la remplacer par une autre.

3° Peux tu m'améliorer la rédaction ? Je veux que ce soit parfait lol.

Sinon autre question :


Soit la fonction x ---> (x+1) / (x^3 - 1). Soit Cf sa courbe représentative.

Étudier la position relative de Cf et de la tangente au point d'abscisse - 1 .

Je trouve comme tangente au point d'abscisse -1 : y = -1/2x - 1/2

On étudie pour la position relative f(x) - y.

On a (x+1) / (x^3 - 1) - ( -1/2x -1/2)
Je trouve sauf erreur de ma part (et je suis sûr qu'il n'y a pas d'erreurs).

x^4 + x^3 +x + 1 / (2(x^3 -1) )

Comment étudier le signe de cette chose ? lol.
Le problème, c'est comment étudier proprement le signe de x4 + x3 +x + 1 qui est toujours positif (ce que je constate avec ma calculatrice), il s'annule également en -1 mais bon c'est pas important.

Merci d'avance.

[Arnaud-29-31]

Oui je me suis planté, bien sur je voulais dire .

Sinon je n'ai pas de TI sous la main donc je ne pas regarder mais ca ne m'étonnerait pas que ce soit possible ^^

Bein pour la rédaction, bien introduire les objets dont on parle puis bien expliquer quoi est quoi et ce qu'on fait.

[Arnaud-29-31]

Pour ton autre exo, je suis d'accord avec l'équation de ta tangente.

Tu as essayé la division euclidienne de par ?
Ou bien en remarquant que ce polynôme admet une racine évident, tu as essayé de la factoriser ?

[Trident]

Oui je me suis planté, bien sur je voulais dire .

Sinon je n'ai pas de TI sous la main donc je ne pas regarder mais ca ne m'étonnerait pas que ce soit possible ^^

Bein pour la rédaction, bien introduire les objets dont on parle puis bien expliquer quoi est quoi et ce qu'on fait.

Merci pour l'aide.

Si ça ne te dérange pas trop de m'aider pour l'étude du signe (demain si tu veux, là je vais dormir), je t'en serais reconnaissant, mais si tu ne veux pas, c'est pas grave, tu m'a déjà assez aidé, j'ouvrirais un nouveau sujet. .

Bonne nuit sinon. :we:

[Trident]

Pour ton autre exo, je suis d'accord avec l'équation de ta tangente.

Tu as essayé la division euclidienne de par ?

Ah merci .

On a pas encore appris la division euclidienne. ^^

[Trident]

Personne pour répondre ???

[Arnaud-29-31]

Ou bien en remarquant que ce polynôme admet une racine évident, tu as essayé de la factoriser ?

Ca ne t'aide pas ?

[Trident]

Regarde le topic "Etude de signe", j'ai marqué ma solution dis moi si c'est juste stp.

[Arnaud-29-31]

Tu fais dans le compliqué alors qu'on peut faire simple.
-1 est racine évidente donc factorise ...

[Trident]

Tu fais dans le compliqué alors qu'on peut faire simple.
-1 est racine évidente donc factorise ...

Oui on a donc par identification (x+1)² ( x² -x +1).

Mais je voudrais quand même savoir si ce que j'ai fait de compliqué est juste.

Et sinon au début j'ai mis (x+1)(ax²+bx+x) et j'ai essayé l'identification, mais je me suis dit on a du x^4 donc ça doit être du (x+1)² mais pourquoi exactement, c'est du (x+1)² ?

[Arnaud-29-31]

Non ce n'est pas ça ... -1 est racine donc on factorise par (x+1).

[Trident]

Non ce n'est pas ça ... -1 est racine donc on factorise par (x+1).

Euh ça c'est juste : (x+1)² ( x² -x +1) , j'ai vérifié.

[Arnaud-29-31]

Oui c'est juste mais -1 racine ne veut a priori pas dire que l'on peut factoriser par (x+1)², pour cela il faut une racine double et a première vu on ne le sait pas ça.

Encore une fois factorise simplement par (x+1) et je te promets que ca saute immédiatement aux yeux que l'expression est positive quelque soit x.

[Arnaud-29-31]

Oui c'est juste mais -1 racine ne veut a priori pas dire que l'on peut factoriser par (x+1)², pour cela il faut une racine double et a première vu on ne le sait pas ça.

Encore une fois, si tu factorises simplement par (x+1), ca saute immédiatement aux yeux que l'expression est positive quelque soit x.

Maintenant après avoir fais ça, tu peux refactoriser par x+1 et obtenir (x+1)².(x²-x+1), cette forme montre aussi très bien que notre expression est positive.

[Trident]

Ok merci bien Arnaud. :lol3: