Petit pb de maths

[bibebule]

j'ai un petit pb, j'ai du mal à commencé mon exercice de math, voici l'intitulé :
La suite (Un) est définie par Uo=1, et Un+1=Un/racine de (Un²+1)

-Prouver par récurrence que Un supérieur à 0
-Prouver que la suite Un est décroissante
-En déduire que la suite Un converge est déterminer sa limite
-Calculer les cinq premiers termes de la suite Un, en vaeurs exactes et faire une conjecture concernat l'expression de Un en fonction de n
-Faire une démonstration par récurrence de cette formule

J'ai vraiment du mal à commencer, si quelqu'un peut me renseigner, se serait gentil. Bis

[Elsa_toup]

Bonjour,

1). Par récurrence:
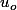=1 > 0.
On suppose que > 0.
Comme , est du signe de , qui est > 0 par hypothèse de récurrence.
Donc > 0.

On l'a montré par récurrence: c'set bon pour tout n !

2). .
Comme (car > 0), , et donc .
Donc .
D'où , soit .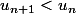

Donc la suite est bien décroissante.

3). est décroissante, minorée par 0, donc elle converge.
On note sa limite.
On a donc : , soit , donc .
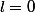Soit , soit , donc , donc , donc .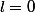

Donc .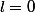

Je te laisse continuer avec ces réponses...
J'espère avoir été claire. :we:

[bibebule]

merci. Mintenan g compri le procédé par récurrence! :id:

[Elsa_toup]

J'en suis ravie !
Parce que tu auras à l'utiliser souvent ... :happy2:

[bibebule]

sinon pr la kestion 2), s ke lon peut utilisé Un+1 - Un pr monter ke la suite est croissante? kar en cours on utilise cete méthode la souven

[Elsa_toup]

Oui c'est la même chose.
Pour montrer qu'une suite est (ici, en l'occurrence) décroissante, on peut faire :
- () et montrer que c'est < 0, donc que .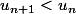
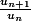- et montrer que c'est < 1, donc que .

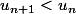On aboutit au même résultat, mais selon la forme de la suite, une des méthodes s'avère souvent plus simple que l'autre.

[bibebule]

a d'accord!
quand on me demande de calculer les cinq premier termes de la suite, en valeurs exactes, on obtient des racines ( ex: pr U1, j'obtien (racine de 2)/2 ) on les laisses omme ca lé résultats?

[bibebule]

parce ke lé résulta sont de plus en plus compliké avec les racines... :!:

[Elsa_toup]

Non, ils disent "en valeurs exactes", ce sera effectivement plus simple.
Donc tu calcules à la calculatrice, et tu prends une valeur approchée à 0,01 par exemple....