Bonsoir,
J'aimerais savoir si mon raisonnement est correct, j'ai un peu de mal avec la récurrence sur des "figures géométriques ".
Soit un carré

, on lui retire un retire un petit carré
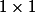
. Montrer que peu importe l'emplacement du petit carre on peut paver le "grand carré moins le petit" avec des "L" (trois carres de coté 1 formant un L).
Je pense que c'est plus simple en généralisant à des carrés de côté une puissance de 2:
Pour un carré de cotés 2x2 c'est évident avec un dessin.
On suppose que c'est vrai pour un carré

et on considère un carré de côté

. On partage ce carre en 4 de

, on applique directement l'hypothèse de récurrence sur le carré où le petit carre est retiré. Pour les trois autres comme l'hypothèse est valable pour n'importe quel emplacement on peut choisir les trois petits carrés de manière a ce qu'il soit adjacents et forment un "L" . Ainsi le grand carre est pavé.
Est-ce correct ? (Dans le fond, la rédaction est pas top du tout!)
