Nombres complexes : modules !

[Shinji]

Voilà l'exercice :
1) Déterminer l'ensemble des nombres complexes z tels que |z|=|1/z|.
2) Déterminer l'ensemble des nombres complexes z tels que |z|=|z+1|.
On pourra poser z= x+iy
3) Quels sont les nombres complexes z tels que z, 1/z et z+1 aient le même module ?

1) j'ai trouvé que l'ensemble des point est le point A d'affixe 1 et le point B d'affixe -1. Et je pense que c'est juste !
2)Là j'ai trouvé que l'ensemble des points est la droite d'équation x=1/2 mais je pense que c'est faux car à cause de ça je n'arrive pas à résoudre la 3) ! :mur:

Alors est ce que mes résultats sont justes, si oui comment résoudre la (3 ?

[annick]

Bonjour,
déjà pour la 1), il faut que tu te souviennes que la/bl = lal / lbl. Avec ça tu dois pouvoir trouver.

[annick]

Bonjour,
oui je suis d'accord avec ta première réponse.
Pour la deuxième, n'est-il pas plus facile de présenter ton équation comme ça : lzl / lz+1l=1 ?

[Shinji]

J'ai un peu de mal avec les modules --' ! Mais le mettre sous cette forme changerai quoi ?

[Nightmare]

Hello,

je ne suis pas d'accord pour la première, tous les points situés sur le cercle unité sont solutions.

[Shinji]

Pourquoi la première serait fausse ?

[annick]

Oups ! Désolée pour ma lecture trop rapide. Effectivement, Nightmare a raison pour la question 1. C'est le module de z qui vaut 1, donc si on associe le point M à l'affixe z, cela veut dire que OM=1, ce qui correspond au cercle (O,1)

[Nightmare]

Eh bien par exemple, il me semble bien que i est aussi solution non? L'équation équivaut à |z|²=1, soit |z|=1 (puisque |z| est un réel positif), c'est à dire que les solutions sont tous les complexes de module 1, c'est bien le cercle unité dans le plan.

[Shinji]

Ok j'ai compris mon erreur ! Et je pense que la deuxième aussi est fausse ! Mais pourquoi mettre module sous cette forme : lzl / lz+1l=1 ?

[Nightmare]

2) peut se résoudre assez bien géométriquement. Si A est le point d'affixe z et B son translaté par la translation de vecteur 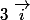dans le repère (l'affixe de B est donc z+1), si |z|=|z+1|, O appartient à la médiatrice du segment [AB]. Comme , dirige la médiatrice de [AB] si bien que O a la même abscisse que le milieu de [AB] (puisqu'ils appartiennent tous les deux à la médiatrice). On doit donc avoir et Re(z+1)=Re(z)+1 et on obtient .

Réciproquement, on vérifie bien que tous les points situés sur la droite d'équation x=-1/2 sont solutions.

[snemder7ay7a]

pas la peine de faire tous cela il faut juste soulever le tout au carré et on trouve le mm resultat

[Shinji]

Ok donc pour la 3) c'est les points qui appartiennent au cercle de centre O et de rayon 1 et a la droite d'équation x=1/2. Il y en a 2 je crois mais peut-on trouver leurs ordonnées par un calcul ?

[Nightmare]

Eh bien, tu sais qu'on a x²+y²= 1 ! et x=1/2 ...

[Shinji]

Ah oui je suis bête --' ! Donc si je me trompe pas: On a 2 point A(1/2; racinede3/2) et B(1/2; - racinede3/2) ?