Narration de recherche

[laurence04]

Bonjour,
j'ai une narration de recherche à faire et j'aimerai avoir l'avis d'autres personnes pour m'aider.

Le Sujet est: parmi tous les rectangles de diagonale 10cm y en a-t-il un qui a un périmètre plus grand que tous les autres?

Personnellement je pense que la réponse est non mais je ne sais pas quoi utilisé comme propriété ou ce genre de données pour le montrer.

Alors est-ce que vous pensez la même chose que moi et pourriez-vous m'apporter de l'aide svp?
Merci d'avance!!!

[Pseuda]

Bonjour,

Je serais plutôt d'avis contraire : un rectangle de diagonale de longueur 10 est inscriptible dans un cercle de diamètre 10 (comme le triangle rectangle correspondant au demi-rectangle). Et on voit bien qu'il y a un maximum quand le sommet du triangle est au-dessus du centre.

[laurence04]

Bonjour,

oui effectivement j'avoue qu'après réflexion plus posée je me suis rendue compte qu'il y a plusieurs rectangles de périmètre différent qui possède une diagonale de 10 cm.

Je compte me poser sur le calcul de périmètre pour trouver le rectangle ayant le périmètre le plus grand.

[beagle]

Par le calcul c'est pas si simple.
Je l'ai fait avec wolfram de deux façons, cela correspond bien au cas de figure donné par Pseuda,
comme on pouvait s'en douter, mais pas si facile à démontrer.
Peut-être si tu as appris courbes croissantes et courbes décroissantes et que tu arrives à démontrer que ...
donc signe de la dérivée etc...

[laurence04]

Bonsoir,

alors merci pour la guidance mais je ne comprends pas le lien entre rectangle, plus grand périmètre et courbes croissantes et décroissantes.

Personnellement, dès que j'ai lu le message j'ai pensé aux limites du fait de devoir trouver LE plus grand périmètre entre chaque rectangle de diagonale 10 cm.

Donc est-ce que vous pourriez m'aider un peu plus car avec votre aide je ne sais pas vraiment où aller.

Un grand merci d'avance!

[beagle]

bah c'est de la faute à Pythagore, à cause de lui on va se trimballer des racines carrées...

Donc tu sais que ta diago est 10.
dans le triangle rectangle de largeur l de longueur L et diago
on a : l² + L² = 10²
donc L² =10² - l²

tu veux du max de périmètre tu veux du max de 2 ( l+L)
bon on peut ne chercher que le max demi périmètre,
on cherche max de l +L
on cherche max de: l + racine carrée de (10²-l²)

alors dans une narration de recherche tu dois dire où tu as trouvé le machin.
Pour ètre honnète j'ai mis cela dans wolfram qui répond:
max (l+ racine carrée (100-l²) = 10racine carrée de 2 at l = 5racine carrée de 2
ce qui est bien le carré comme défini par pseuda.

alors que se passe-t-il:
si on étudie une courbe du rectangle
on démarre avec un rectangle très aplati, horizontal, qui est très proche d'un périmètre de 10+10

Plus on écarte la largeur, plus le périmètre croit (croissance de la fonction)
On atteint un maximum avec le carré
Puis le rectangle tend vers du raplapla, la largeur devient longueur, la longueur devient largeur,
et on va vers un rectangle tout mince vertical cette fois -ci qui tend vers le 10+10 également.

Bref on a eu une courbe croissante jusqu'au max et décroissante à partir du max.

Mathématiquement je sais pas faire.
Mais une fonction pour savoir si elle est croissante ou décroissante on étudie le signe de sa dérivée.

Donc si tu sais dériver les racines carrées, vas-y.perso je ne sais pas faire
tu devrais trouver 1- l/ racine carrée de (100-l²)
tu bosses ce truc tu regardes de quand positif cela devient négatif, cela se joue à l²=50

Un autre truc pour croissant décroissant c'est
si a inf b alors f(a) inf f(b) , ça n'a pas l'air simple.

[beagle]

sinon j'ai joué aussi avec le triangle dans le cercle comme le dit Pseuda
tu mets un diamètre la diago
tu prends un point du cercle, cela tet fait un triangle rectangle.
J'avais noté x le déplacement de la hauteur du triangle sur le diamètre.
x se ballade de 0 à 10
tu peux exprimer le périmètre du triangle en fonction de x
cela doit ètre
l= racine carrée de 10x
et L = racine carrée de 10(10-x)
alors tu cherches max de
racine carrée de x + racine carrée de (10-x)

bref c'est comme tout à l'heure tu te trimbales des sommes de racines carrées.
Donc pour moi qui suis un incapable ou un ignorant ben je suis pas plus avancé
wolfram dit global maximum at x =5
donc la hauteur passe par le milieu du diamètre = on est dans la configuration du carré.

[samoufar]

Bonsoir,

Au contraire, c'est Pythagore qui nous sauve Il y a une méthode pour y arriver, plutôt naturelle mais loin d'être évidente. Il faut voir comme l'équation d'un cercle.

Dès lors, en normant (càd en posant et ), on se ramène à l'équation .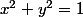

Ce qui est sympa ici, c'est qu'on peut réécrire l'équation avec un seul paramètre , pour lequel l'équation devient plus simplement...



Il suffit alors de trouver la valeur de qui maximise la fonction (à savoir le périmètre à une constante multiplicative près qui doit valoir 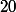je crois).

Pour ça, on résout l'équation et on remonte les calculs


J'avoue que, niveau lycée, c'est un peu délicat (surtout qu'il faut connaître l'équation d'un cercle)

[Ben314]

Salut,

Capture.png (26.6 Kio) Vu 393 fois

Je sais pas si ça peut servir dans une "narration de recherche", mais on peut éventuellement le faire avec du "pur géométrique" a condition de connaitre le Théorème de l'angle inscrit (vu au Lycée ?)
On fait la construction comme çi dessus avec A,C,O, fixés, B variable sur le cercle 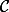de diamètre [AC] et A', B' les points tels que BAA'B' soit un carré (extérieur au rectangle)
L'angle CB reste constant égal à CA (Th de l'angle inscrit) donc égal à 45° ce qui montre que , B et A' sont alignés (l'angle ABC est droit et l'angle ABA' vaut 45°)
La droite (A'B) est la médiatrice de [AB'] et, comme est sur cette médiatrice, c'est que A=B' ce qui signifie que B' se balade sur le cercle 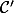de centre passant par A.
Or, la distance CB' est égale à CB+BA, c'est à dire au demi périmètre du rectangle.
Il faut donc chercher le point B' du cercle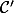 qui soit le plus éloigné possible du point C et, comme C est lui même sur 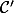, ce point le plus éloigné est le symétrique de C par rapport au centre du cercle et il suffit de prendre B= pour l'obtenir.

Si le théorème de l'angle inscrit n'est pas vu au Lycée, il peut éventuellement y avoir un autre moyen de montrer que B' se balade sur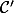 : peut-être en considérant le symétrique E de C par rapport à on arrive à montrer que l'angle CB'E est droit ce qui montrerais que B' est sur le cercle de diamètre [CE]...

[laurence04]

Bonsoir,

Je vous remercie infiniment pour les aides car je comprends mieux vers quel chemin me tourner même si il y a certaines choses que je comprends pas (car pas vu au lycée). Mais j'ai compris l'ensemble des idées, donc maintenant je vais concocter cela de ma manière, en utilisant un peu de tout ce que vous m'avez dit. Bien sûr de façon logique, et non au hasard!!

Merci vraiment!!!

[Ben314]

Un truc qui peut être marrant si tu as rien d'autre à f..., c'est de faire un "modèle concret" pour rendre compte du problème :
Tu prend deux bouts de bois de même longueur (ou des pièces de Mecano ou de Lego ou je sais pas quoi d'un peu rigide) que tu perce en leur milieu et tu met un boulon dans les deux trous de façon à ce que les morceaux de bois puissent pivoter l'un par rapport à l'autre (ou tu met un clou ou.. autre chose).
Tes deux bouts de bois matérialisent alors les diagonales de ton rectangle et si tu plante des clous aux extrémités des deux bouts de bous et que tu relie les clous avec des élastiques (un grand ou plusieurs petits), ça "matérialise" les cotés de ton rectangle.
Et si à la place des élastique, tu met une ficelle + un petit morceau d'élastique, tu verra relativement bien dans quelle disposition l'élastique est le plus "distendu" ce qui correspond au périmètre maximal pour ton rectangle.
Tu peut aussi constater que l'élastique à évidement tendance à vouloir diminuer le périmètre donc que si dans une disposition donnée des bout de bois l'élastique ramène les bois de bois dans un certain sens, ça signifie qu'une modification dans ce sens là fait diminuer le périmètre.

Et avec tes deux malheureux bouts de bois et tes clous, tu peut faire pas mal de "petites expériences" qui permettent d'assez bien visualiser le problème.