Moyenne pondérée et écart type pondéré

[maniqk]

Bonjour,
Je souhaitais calculer la moyenne d'un échantillon, connaissant la moyenne de chacun des sous échantillons ainsi que le nombre de points dans chacun des échantillons. La moyenne pondérée a répondu à mon besoin.

De la même manière, je cherche à calculer l'écart type d'un échantillon, connaissant l'écart type de chacun des sous échantillons, et le nombre de points de chaque échantillon. Existe t'il une formule permettant de faire ce calcul ?
Je vous mets un exemple simple en PJ. Je cherche à retrouver la valeur de 5.91, en connaissant l'écart type de chacun des échantillons, et éventuellement leur moyenne. J'ai trouvé une formule (que j'ai mis dans la PJ également), mais je ne parviens pas à l'appliquer.
Sauriez-vous m'aider ?

Merci d'avance !

[GaBuZoMeu]

Bonjour,

Quelle pièce jointe ?

Reviens aux définitions : la variance est la moyenne des carrés moins le carré de la moyenne. Quand tu as des échantillons de tailles différentes, tu pondères les moyennes. Ça devrait te permettre de t'y retrouver ?

[maniqk]

Bonjour,
Je n'arrive pas à joindre les PJ...
Désolé pour la forme mais voilà mon exemple :
ECHANTILLON 1
1
2
3
4
5
6
ECHANTILLON 2
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ECART TYPE du total = 5.91
ECART TYPE échantillon 1 = 1.87
ECART TYPE échantillon 2 = 4.18
MOYENNE échantillon 1 = 3.5
MOYENNE échantillon 2 = 13.5
nombre de points échantillon 1 = 6
nombre de points échantillon 2 = 14

[GaBuZoMeu]

Je t'ai donné une piste.

[maniqk]

Bonjour,
Merci pour la piste mais je n'y parviens pas...
Si je dispose de ces données :
ECART TYPE du total = 5.91
ECART TYPE échantillon 1 = 1.87
ECART TYPE échantillon 2 = 4.18
MOYENNE échantillon 1 = 3.5
MOYENNE échantillon 2 = 13.5
nombre de points échantillon 1 = 6
nombre de points échantillon 2 = 14

et que j'applique la définition :
moyenne des carrés = (1.87² + 4.18²)/2 = 10.48
carré de la moyenne = ((1.87 + 4.18)/2)² = 9.15
variance = 10.48 - 9.15 = 1.33
soit écart type = 1.16 <> 5.91 recherché

Mais je n'ai pas utilisé de pondération. J'ai alors tenté de cette façon :
moyenne des carrés = (6*1.87² + 14*4.18²)/2 = 132.8
carré de la moyenne = ((6*1.87 + 14*4.18)/2)² = 1215.92
et je m'arrête là car je vois que je vais avoir un problème pour la suite...
Je pense que je pondère mal mes données, pourrais-tu m'aiguiller ?

Pour mes calculs ci-dessus j'ai utilisé les écart type de chacun des échantillons, j'ai également tenté avec les moyennes mais je ne retrouve pas ma valeur de 5.91

[catamat]

Bonjour

Si vous avez du mal, commencez par la moyenne c'est plus facile (nettement)

Voici un exemple
Echantillon 1 : 5,6,7, soit 3 valeurs de moyenne x1=6
Echantillon 2: 12,16, soit 2 valeurs de moyenne x2=14

Pour calculer la moyenne générale il faut récupérer la somme totale et diviser par 5
La somme des valeurs est 5+6+7+12+16 mais aussi 3*6+2*14 ou encore 3*x1+2*x2
Donc c'est (3*x1+2*x2)/5
Faites déjà cela pour la moyenne.

[maniqk]

Bonjour catamat,
J'ai fait le calcul pour la moyenne avec mon exemple qui en effet est beaucoup plus simple.
Avec mon exemple, la moyenne pondérée vaut (6*3.5 + 14*13.5)/(6+14) = (21+189)/20 = 10.5
Qui est bien la moyenne de [1, 2, 3.. 20].

Mais le même raisonnement ne semble pas s'appliquer pour l'écart type :
(6*1.87 + 14*4.18) /(6+14) = 3.49
Mais l'écart type du total vaut 5.91.
C'est probablement ma formule qui n'est pas bonne mais je ne sais pas ce qui ne va pas...

[lyceen95]

L'écart-type , c'est compliqué. Oublie pour l'instant, fait comme si ça ne t'intéressait pas.
La variance, c'est simple. C'est plus compliqué que la moyenne, certes, mais c'est abordable.

Et quand tu auras la variance, tu as une formule immédiate pour en déduire l'écart-type. Et donc pour solutionner ton problème.

[catamat]

En effet la variance comme le rappelle Mathelot c'est la moyenne des carrés moins le carré de la moyenne.

La moyenne des échantillons, on connait, donc on peut en déduire la moyenne des carrés de chaque échantillon puis la moyenne des carrés de l'ensemble des résultats (même méthode que pour la moyenne simple )

Ensuite on en déduit la variance et donc l"écart type de l'ensemble des résultats.

[lyceen95]

Et la moyenne des X², c'est ?
C'est la somme des X², divisée par le nombre de X².
On doit donc calculer des sommes , ou des nombres d'éléments. Ca doit pouvoir se faire.

[maniqk]

En appliquant la définition variance = moyenne des carrés moins carré de la moyenne avec mon échantillon qui va de 1 à 20, je trouve :
moyenne des carrés = (1² + 2² + ... + 20²)/20 = 2870/20 = 143.5
carré de la moyenne = ((1+2+...+20)/20)^2 = 10.5² = 110.25
donc variance = 143.5 - 110.25 = 33.25
d'où écart type = racine carrée de la variance = 5.77

Ce calcul est il juste ? Car avec Excel, en utilisant l'écart type standard, le calcul donne écart type = 5.91

En raisonnant avec les échantillons, je trouve :
moyenne des carrés = (3.5² + 13.5²)/2 = 97.25
carré de la moyenne = ((3.5+13.5)/2)² = 72.25
soit variance = 25 et écart type = 5

Et je ne retrouve toujours pas mon 5.91 qu'Excel fournit

[maniqk]

Désolé je viens tout juste de tester la fonction Excel ECARTTYPE.PEARSON qui me renvoie bien le 5.77.
C'est donc cette valeur que je cherche à retrouver en ne connaissant que la taille des échantillons, leur moyenne, et éventuellement la variance et l'écart type de chacun des échantillons (je ne connais pas les valeurs dans chacun des échantillons)

[lyceen95]

Tu tombes sur un autre problème.

Il y a 2 ""écoles"" pour le calcul de l'écart-type ... et ça se justifie. Je ne vais pas entrer dans cette explication ici.
Les 2 formules ont certainement des noms différents, mais je ne m'en souviens plus.

Pour une variable X, pour laquelle on a N observations :

Etape 1, commune aux 2 écoles : on calcule la moyenne de tous les X, et je note cette moyenne X0
Etape 2, commune aux 2 écoles : on calcule la somme des (X-X0)²
Etape 3, et c'est là qu'on a une différence : on divise soit par N, soit par (N-1)
Etape 4 : on prend la racine carrée du résultat.

Sur ton exemple, on vérifie bien que (5.91/5.77)² = 20/19 aux arrondis près.

Quand tu as tes écarts-type pour tes 2 sous-groupes, tu as besoin de savoir comment ils ont été calculés (laquelle des 2 écoles).
Quand tu sais ça, tu sais reconstituer la somme des (X-X0)² dans chacun des 2 sous-groupes. Et c'est ça qui est utile. C'est ça que tu vas pouvoir réutiliser pour calculer la somme des (X-X0)² sur le total des 2 sous-groupes ... et faire tous les calculs.

[maniqk]

Merci pour les explications sur les différences
A priori la définition variance = moyenne des carrés moins carré de la moyenne correspond à l'ECARTYPE.PEARSON d'Excel, c'est celle que je vais utiliser pour le reste de mes calculs.

Par contre je ne comprends toujours pas comment retrouver ma variance du groupe total...
Groupe = [1,2,3...,19,20]
SG1 = [1,2,..6] et SG2 = [7,8..,20]
moyenne Groupe = 10.5
moyenne SG1 = 3.5
moyenne SG2 = 13.5

variance Groupe = 33.25 = [ (1-10.5)² + (2-10.5)² + ... + (20-10.5)² ] / 20
variance SG1 = 2.92 = [ (1-3.5)² + (2-3.5)² + ... + (6-3.5)² ] / 6
variance SG2 = 16.25 = [ (7-13.5)² + (8-13.5)² + ... + (20-13.5)² ] / 14

Je ne vois pas le lien entre les différences variances... J'ai testé cette pondération :
(6*2.92 + 14*16.25)/20 = 12.25 <> 33.25

Je ne sais pas si j'étais clair mais je ne dispose pas de toutes les valeurs de chaque sous-groupe, car mon but final est de pouvoir calculer l'écart type d'un groupe très grand, connaissant uniquement certaines statistiques des sous-groupes qui le composent.
Pour mon exemple, je connais uniquement la moyenne et la variance de chaque sous-groupe, mais pas les valeurs qui composent le sous-groupe.

[Vassillia]

Bonjour,

@maniqk

Autrement dit
De même

Donc
On a enfin obtenu la somme des carrés, il reste à la diviser par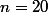
Comme on a aussi la moyenne du groupe, on peut la mettre au carré et je te laisse finir


@Lyceen95 Je vois ce que tu veux dire mais parler de 2 écoles est un peu maladroit, tout le monde est d'accord (enfin sauf qui tu sais qui va encore faire des siennes mais bon )
Pour un échantillon, ce qui veut dire mathématiquement une suite de variables aléatoires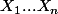 indépendantes et identiquement distribuées selon une loi inconnue qui possède une espérance et une variance
La moyenne empirique est un estimateur sans biais et convergent vers
La variance empirique est un estimateur convergent vers mais problème il n'est pas sans biais ce qui veut dire que

Démonstration pour le fun

car et 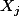sont indépendantes
Au final




Pour le corriger, il faut donc multiplier notre estimateur ce qui donne la variance empirique sans biais

[lyceen95]

Allons-y.

Je vais noter M1 la moyenne du groupe 1, M2 la moyenne du groupe 2 et M0 la moyenne du groupe(1+2).
Et avec la même logique : N1 l'effectif du groupe 1, N2 et N0 ...
S1: la somme des éléments du groupe 1 et S2 S0 ...
S1 et S2 ne sont pas donnés au départ, mais on sait que S1=M1*N1 et S2=M2*N2

Donc le premier résultat simple, c'est que S0 = S1+S2.
Je préfère travailler avec S0 S1 et S2, plutôt que M0 M1 et M2, parce que S0 se calcule par une simple addition.
Je veux manipuler uniquement des données sommables (S0=S1+S2 , facile, N0=N1+N2, facile, M0=... pas facile donc je me débarasse des moyennes, je m'intéresse uniquement aux indicateurs sommables)

Maintenant, attaquons les données relatives aux variances.
On a ECT1 et ECT2, les écart-types des groupes 1 et 2.
On en déduit VAR1 et VAR2, les variances des groupes 1 et 2 : VAR1=(ECT1)²
Par ailleurs, VAR1, c'est la moyenne des carrés des écarts à la moyenne. C'est la définition de la variance.
Mais tu dois savor que le calcul se simplifie, et que la variance, c'est la moyenne des carrés, moins le carré de la moyenne. VAR = E(X²) - (E(X) )²
Donc N1 * VAR1, c'est N1* E(X1²) -N1* (E (X1))²
J'ai des moyennes. Comme déjà dit, je n'aime pas les moyennes, je fais apparaitre Sommes et effectifs, plutôt que moyennes :
C'est donc N1 * VAR1 = Sum( X1²) - N1 * ( S1 /N1) ²
N1 * VAR1 = Sum( X1²) - S1² /N1

On connait N1, on connait VAR1, on connait S1 ... on en déduit Sum(X1²) ( en espérant que les notations sont claires)
Pareil pour le 2ème sous groupe , on peut trouver Sum(X2²)

Quand on a trouver Sum(X1²) et Sum(X2²) , on additionne ces 2 nombres, et ça nous donne Sum(X0²).

Quand on a sum(X0²), et S0 et N0 ... on peut calculer notre variance sur l'effectif total : VAR0 =Sum(X0²)/N0 -(S0/N0)²
Puis ECT0 = racine(VAR0)

Mets tout ça dans un tableur, tu verras, ce sera beaucoup plus clair.

L'idée dans tous ces calculs, c'est la même de bout en bout. Quand on a une moyenne, il faut tout de suite se dire qu'une moyenne, c'est une somme divisée par un effectif.
Pareil pour une variance, c'est la somme de ... moins la somme de ... divisée par l'effectif de ....

On ne manipule que des sommes et des effectifs (somme des X, somme des X² ) ; quand on connait Somme des X et Somme des X² sur chacun des 2 groupes , on en déduit ces indicateurs sur le cumul, par une simple addition. Et c'est fini.


Edit :
Vassilia : oui ... l'histoire des 2 écoles est maladroite. Disons 2 contextes différents, qui font qu'on doit utiliser parfois une formule, parfois une autre.

[maniqk]

Bonjour,
Merci beaucoup à tous les 2 pour vos réponses. Je constate en effet que ça marche parfaitement... Très honnêtement je n'y serai pas parvenu ! La prépa remonte déjà à 13 ans et j'ai perdu pas mal en raisonnement

Je peux résumer le tout avec la formule suivante :
VAR_total = [Somme(N_i * Var_i) + (S_i²/N_i)] / N + (Somme(x_i) / N)²
où :
x_i = valeurs constituant le groupe i
N_i = effectif du groupe i
N = effectif de l'échantillon total = somme des N_i
Var_i = variance du groupe i
S_i = somme des valeurs constituant le groupe i

Une toute dernière question par rapport à la démonstration : @lyceen95, tu as mis :
N1 * VAR1 = N1* E(X1²) -N1* (E (X1))²
N1 * VAR1 = Sum( X1²) - N1 * ( S1 /N1) ²
Je comprends l'égalité E(X1) = (S1/N1), mais pourquoi est ce que N1*E(X1²) = Sum(X1²) ?

[maniqk]

Je me suis trompé dans la formule. La formule correcte est :
VAR_total = [ Somme(N_i*Var_i + S_i²/N_i) ] / N - (Somme(S_i) / N)²

[maniqk]

J'ai tenté la formule avec les deux "écoles". Ça marche bien pour l'écart type PEARSON (en divisant par N), mais un peu moins bien pour l'écart type STANDARD (en divisant par N-1).

Cas PEARSON avec mon exemple :
Var({1,2,3,4,5,6}) = 2.917
Var({7,8,...,20}) = 13.5
Var_total = [6*2.917 + 14*13.5 + 21²/6 + 189²/14] / (6+14) - ((21+189)/(6+14))² = 33.25
Et on peut vérifier que Var({1,2,3,...,20}) = 33.25

Cas STANDARD :
Var({1,2,3,4,5,6}) = 3.5
Var({7,8,...,20}) = 17.5
Var_total = [5*3.5 + 13*17.5 + 21²/5 + 189²/13] / (5+13) - ((21+189)/(5+13))² = 35.05
Mais Var({1,2,3,...,20}) = 35 tout pile
Est ce simplement une erreur d'arrondis ? Ou est ce qu'il y a des coefficients que j'utilise et qui ne sont pas bons ?