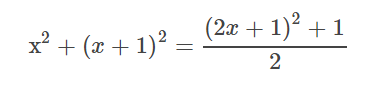Montrer une égalite (équation, 1ère)

[Youyou1617]

Bonjour,
un exercice me demande de montrer une égalité, ce que je ne parviens pas a faire.
J'ai essayé la factorisation, le développement et trouvé des identités remarquables dans les deux expressions mais cela n'aboutit à rien.
Voici l'égalité en question:

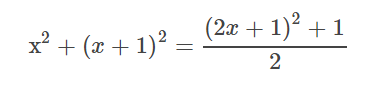
Merci beaucoup de votre aide !

[pascal16]

tu développes les carrés de chaque coté.
tu rassembles les x² de gauche ensemble, les x de gauche ensembles, et les constantes de gauche ensembles.
pareil coté droit
tu doit voir les deux m^me choses écrites de chaque coté

[Youyou1617]

bonjour,
lorsque je développe de chaque coté, le résultat n'est pas bon.
Pourriez vous m'expliquer qu'entends vous par développer les carrés ?
Voici mon calcul:
x^2+(x+1)^2=((2x+1)^2+1)/2
x^2+x^2+2x+1 = (4x^2+4x+2)/2 (identités remarquables)
2x^2+2x+1 = 4x^2+4x+1
arrivé la je ne sais plus quoi faire..
Merci

[annick]

Bonjour,

je ne comprends pas bien tes calculs :

x²+(x+1)²= x²+x²+2x+1=2x²+2x+1

((2x+1)^2+1)/2= (4x^2+4x+2)/2 =2x²+2x+1 (c'est là que tu as fait une erreur de calcul)

Donc les deux membres sont bien égaux.

[lyceen95]

Pour que ta copie soit lisible, il faut prendre l'expression de gauche et la transformer jusqu'à un truc simple.
Et idem prendre l'expression de droite et la transformer jusqu'à un truc simple.
Et à la fin, constater que les 2 trucs simples en question, ils sont égaux.

Comme fait par Annick.

[Youyou1617]

bonsoir,
c'est bon j'ai compris ou est mon erreur, il fallait que je divise toute l'expression de droite par deux une fois le numérateur factorisé, au final ce n'était pas si compliqué..
Merci à vous !