Bonjour
Pour le titre d'un paragraphe que je dois écrire (pour voir si je comprends je fais des petits exos en plus des exos que je trouve ailleurs)
Donc bref dans mon premier paragraphe je parle des matrices inversibles puis au second paragraphe je parle des matrices qui possèdent le même nombre de lignes que leur rang (et sont inversibles si elle sont carrées donc du coup)
Comment appeler une matrice de même rang qu'elle possède de lignes (ou alors de colonne)?
Appeler ça une matrice d'une sous base ( si elle est carrée ça sera la matrice d'une base) ça le fait?
Np matrice de rang n ou p
9 messages
- Page 1 sur 1
Re: np matrice de rang n ou p
Salut,
Perso, une matrice dont le rang est égal à son nombre de ligne ou à son nombre de colonne (forcément le plus petit des deux), j'aurais tendance à appeler ça une "matrice de rang maximal".
Perso, une matrice dont le rang est égal à son nombre de ligne ou à son nombre de colonne (forcément le plus petit des deux), j'aurais tendance à appeler ça une "matrice de rang maximal".
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: np matrice de rang n ou p
Merci Ben 314
Donc c'est comme ça que cela s'appelle (moi j'y connais rien j'essaye juste de refaire mes exos avec des remarques que je place à coté)
Donc c'est comme ça que cela s'appelle (moi j'y connais rien j'essaye juste de refaire mes exos avec des remarques que je place à coté)
Re: np matrice de rang n ou p
...et en plus c'est logique de l'appeler comme ça
donc bref merci Ben 314
donc bref merci Ben 314
Re: np matrice de rang n ou p
Salut donc du coup mon texte c'est ça (le deuxième paragraphe parlant des matrices de rang maximal)
si des fois que ça tente quelqu'un de voir si j'ai fait des fautes...(mais bon ça saoule -...faut vraiment avoir envie de
"lire" )
-Matrices de)
Préalablement pour on choisira le corps
on choisira le corps 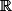 ou le corps
ou le corps 
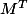 désigne la matrice transposée de
désigne la matrice transposée de 
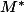 désigne la matrice adjointe de
désigne la matrice adjointe de 
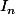 désigne la matrice identité d'ordre
désigne la matrice identité d'ordre 
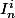 désigne la matrice colonne qui est la
désigne la matrice colonne qui est la  -ième colonne de la matrice identité d'ordre
-ième colonne de la matrice identité d'ordre 
Éventuellement on écrira à la place de
à la place de  quand il n'y aura pas de confusion possible en ayant préalablement dit de quel ordre est la matrice identité
quand il n'y aura pas de confusion possible en ayant préalablement dit de quel ordre est la matrice identité
Par conséquent\) et
et ^*\ =\ \left(I_n^i\right)^T\ \in \ \mathcal {M}_{1,n}\left(K\right)\)
Formules élémentaires
Soit\) de coefficients
de coefficients 
^*\ M\ \left(I_p^j\right)\) est la matrice carrée d'ordre l'unité et de coefficient
est la matrice carrée d'ordre l'unité et de coefficient 
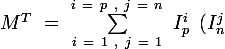^*\ M\ I_p^i\ \left(I_n^j\right)^*)
§1.Matrices de permutation
Soit est une matrice de permutation d'ordre
est une matrice de permutation d'ordre  et de coefficients
et de coefficients 
Donc)
Les coefficients de sont zéro et un
sont zéro et un
Il n'y a qu'un seul par ligne et par colonne
par ligne et par colonne
Les matrices de permutation d'ordre sont associées aux permutation de
sont associées aux permutation de 
À on associe la matrice de permutation
on associe la matrice de permutation  telle que
telle que 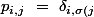}\)
Avec le symbole de Kronecker où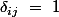 ssi
ssi 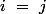 sinon
sinon 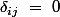
L'ensemble des matrices de permutation d'ordre muni de la multiplication matricielle est un groupe isomorphe à
muni de la multiplication matricielle est un groupe isomorphe à  et dont l'élément neutre est la matrice identité
et dont l'élément neutre est la matrice identité 
§1a.
On montre qu'une matrice de permutation est inversible
Son déterminant vaut la signature\)
Démonstration
Le calcul de la signature compte le nombre de permutations depuis l'ordre originel\) et on sait qu'à chaque fois qu'on permute les lignes (ou les colonnes) on change le signe du déterminant
et on sait qu'à chaque fois qu'on permute les lignes (ou les colonnes) on change le signe du déterminant
De plus on montre que le déterminant d'une matrice de permutation vaut ou
ou 
Elle est donc inversible
Comme le déterminant du produit de deux matrices carrées est le produit des déterminants de ces deux matrices et comme les matrices de permutation d'ordre forment un groupe fini isomorphe à
forment un groupe fini isomorphe à  alors le déterminant de la chaîne constituée d'un produit de matrices de permutation ne peut avoir d'autre valeur que
alors le déterminant de la chaîne constituée d'un produit de matrices de permutation ne peut avoir d'autre valeur que  ou
ou 
§1b.
On montre que si et
et  sont dans
sont dans  alors
alors 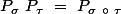
Démonstration
Évident puisque le groupe formé des matrices de permutation d'ordre est isomorphe à
est isomorphe à 
§1c.
On montre que l'inverse d'une matrice de permutation est sa transposée
Démonstration
Soit de coefficients
de coefficients  est une matrice de permutation et calculons le produit de celle-ci avec sa transposée
est une matrice de permutation et calculons le produit de celle-ci avec sa transposée 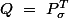 de coefficients
de coefficients  et notons
et notons  les coefficients du produit
les coefficients du produit 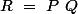
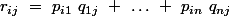 avec
avec 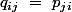
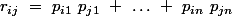 avec
avec 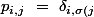})
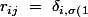}\ \delta _{j,\sigma \left(1\right)}\ +\ \ldots \ +\ \delta _{i,\sigma \left(n\right)}\ \delta _{j,\sigma \left(n\right)})
 tel que
tel que 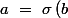)
}\ \delta _{j,\sigma \left(b\right)}\ =\ \delta _{a,a}\ \delta _{j,a})
et comme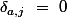 si
si 
 sont les coefficients de la matrice identité
sont les coefficients de la matrice identité
§1d.
Le seul coefficient de valeur un de la colonne de
de  est situé à la ligne
est situé à la ligne \) de cette colonne là
de cette colonne là
Par exemple
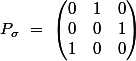
Par conséquent
\ =\ 3)
\ =\ 1)
\ =\ 2)
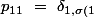}\ =\ \delta _{13}\ =\ 0)
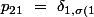}\ =\ \delta _{23}\ =\ 0)
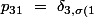}\ =\ \delta _{33}\ =\ 1)
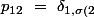}\ =\ \delta _{11}\ =\ 1)
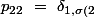}\ =\ \delta _{21}\ =\ 0)
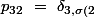}\ =\ \delta _{31}\ =\ 0)
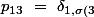}\ =\ \delta _{12}\ =\ 0)
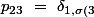}\ =\ \delta _{22}\ =\ 1)
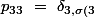}\ =\ \delta _{32}\ =\ 0)
Soit\) une matrice carré de coefficients
une matrice carré de coefficients 
On montre que la -ième colonne de
-ième colonne de  est la
est la ) -ième colonne de
-ième colonne de 
et la -ième ligne de
-ième ligne de  est la
est la ) -ième ligne de
-ième ligne de 
Démonstration
Soit de coefficients
de coefficients  est une matrice de permutation et calculons
est une matrice de permutation et calculons 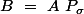 de coefficients
de coefficients 
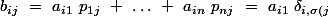}\ +\ \ldots \ +\ a_{in}\ \delta _{n,\sigma \left(j\right)})
 tel que
tel que 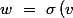)
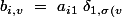}\ +\ \ldots \ +\ a_{iw}\ \delta _{w,\sigma \left(v\right)}\ +\ \ldots \ +\ a_{in}\ \delta _{n,\sigma \left(v\right)}\ =)
}\ =\ a_{i,\sigma \left(v\right)}\ \delta _{\sigma \left(v\right),\sigma \left(v\right)}\ =\ a_{i\sigma \left(v\right)})
À présent calculons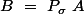
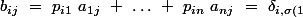}\ a_{1j}\ +\ \ldots \ +\ \delta _{i,\sigma \left(n\right)}\ a_{nj})
 tel que
tel que 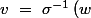)
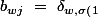}\ a_{1j}\ +\ \ldots \ +\ \delta _{w,\sigma \left(v\right)}\ \ a_{vj}\ +\ \ldots \ +\ \delta _{w,\sigma \left(n\right)}\ \ a_{nj}\ =)
}\ a_{vj}\ =\ \delta _{w,w}\ a_{vj}\ =\ a_{\sigma ^{-1}\left(w\right),j})
§1e.
Si est la résultante d'une permutation
est la résultante d'une permutation  des colonnes (resp. des lignes) d'une matrice inversible
des colonnes (resp. des lignes) d'une matrice inversible  alors
alors  est la résultante de la même permutation
est la résultante de la même permutation  des lignes (resp. des colonnes) de la matrice
des lignes (resp. des colonnes) de la matrice 
Démonstration
Évident selon^{-1}\ =\ \left(P_{\sigma }\ A\right)^{-1}\ P_{\sigma }\ =\ A^{-1})
§2.Matrices de rang maximal
Soit est une matrice de
est une matrice de  lignes,
lignes, 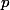 colonnes à coefficients dans
colonnes à coefficients dans  et de rang non nul
et de rang non nul 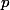
Donc\ ,\ Rg\left(A\right)\ =\ p\in \mathbb {N}^*)
§2a.
On montre que l'on vérifie l'équivalence:

Démonstration:
D'une part on vérifie toujours l'implication
D'autre part comme\) , si
, si  est carrée alors
est carrée alors 
et on sait que toute matrice d'ordre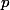 et de rang
et de rang 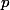 est inversible
est inversible
§2b.
On montre que l'on vérifie
Démonstration:
Supposons que et on sait que
et on sait que \)
par conséquent\ \leq \ min\left(n\ ,\ p\right)\)
si on suppose que alors
alors \ =\ n\) et donc
et donc \ \leq \ n\)
mais le contexte est que\ =\ p\) ce qui contredit ce que l'on a supposé
ce qui contredit ce que l'on a supposé
§2c.
On montre qu'il existe une matrice inversible d'ordre
d'ordre 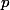 telle que toutes ses colonnes sont aussi des colonnes de la matrice
telle que toutes ses colonnes sont aussi des colonnes de la matrice 
Démonstration:
\ =\ Rg\left(A^T\right)\) donc
donc \ =\ p\) et
et \)
il existe donc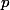 vecteurs colonne de
vecteurs colonne de  de la matrice
de la matrice  qui forment un système de vecteurs libres et donc engendrent
qui forment un système de vecteurs libres et donc engendrent 
§2d.
On se donne la matrice inversible d'ordre
d'ordre 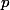 telle que toutes ses colonnes sont aussi des colonnes de la matrice
telle que toutes ses colonnes sont aussi des colonnes de la matrice 
Au paragraphe précédent on a vu qu'une telle matrice existe
Et on se donne la matrice\) qui vérifie l'équivalence suivante:
qui vérifie l'équivalence suivante:
\ \Longleftrightarrow \)
)
On montre que l'on vérifie
Démonstration:
Notons les coefficients de la matrice identité
les coefficients de la matrice identité  d'ordre
d'ordre  avec
avec  et
et 
Cette notation très peu pratique est choisie malgré tout car est la seule matrice identité que l'on aura besoin ici
est la seule matrice identité que l'on aura besoin ici
Donc en considérant le symbole de Kronecker on a l'égalité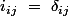
Et notons les coefficients de
les coefficients de  $ avec $
$ avec $ $ et $
$ et $
Là encore cette notation est à priori très peu pratique mais comme on va le voir elle ne sert juste qu'à dire que le coefficient est un coefficient de
est un coefficient de  sans rentrer dans le détail de la transposition de la matrice
sans rentrer dans le détail de la transposition de la matrice 
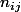 les coefficients de
les coefficients de 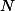 avec
avec  et
et 
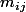 les coefficients de
les coefficients de  avec
avec  et
et 
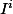 la
la  -ième colonne de
-ième colonne de  avec
avec 
 la
la  -ième colonne de
-ième colonne de  avec
avec 
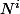 la
la  -ième colonne de
-ième colonne de 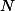 avec
avec 
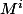 la
la  -ième colonne de
-ième colonne de  avec
avec 
Selon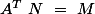 que l'on doit démontrer il faut donc vérifier
que l'on doit démontrer il faut donc vérifier
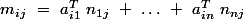 avec
avec  et
et 
Par ailleurs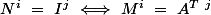
et on sait que toutes les colonnes de sont aussi des colonnes de
sont aussi des colonnes de 
on peut poser l'injection définie par
définie par 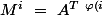})
de sorte que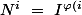}\ \Longleftrightarrow \ M^i\ =\ A^{T\ \varphi \left(i\right)})
et par conséquent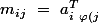})
par ailleurs on vérifie aussi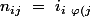}\ =\ \delta_{i\ \varphi \left(j\right)})
On arrive donc à l'égalité à démontrer suivante:
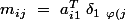}\ +\ \ldots \ +\ a^T_{in}\ \delta _{n\ \varphi \left(j\right)}\) avec
avec  et
et 
par ailleurs comme est une application de
est une application de  dans
dans  alors pour tout
alors pour tout  dans
dans  il existe
il existe  dans
dans  tel que
tel que 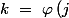\) et comme
et comme }\ =\ 1\) uniquement si
uniquement si 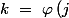\) et sinon
et sinon }\ =\ 0\) on a donc:
on a donc:
}\ =\ a^T_{i\ \varphi \left(j\right)}\ \delta _{\varphi \left(j\right)\ \varphi \left(j\right)}\ =\ a^T_{i\ \varphi \left(j\right)}\) et on va vu que
et on va vu que 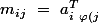})
§2e.
Soit une matrice de permutation d'ordre
une matrice de permutation d'ordre 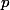
Et posons la matrice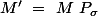
Et considérons la matrice qui vérifie l'équivalence
qui vérifie l'équivalence
\ \Longleftrightarrow \)
)
Alors on montre d'une part que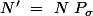
et d'autre part on vérifie l'égalité^T\ N^{\prime \ T}\ =\ \left(M^{-1}\right)^T\ N^T)
Démonstration
Il est évident que la matrice de permutation permute les mêmes colonnes de et
et 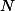
De sorte qu'en posant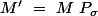 et
et 
^T\ N^{\prime \ T}\ =\ \left(\left(M\ P_{\sigma }\right)^{-1}\right)^T\ \left(N\ P_{\sigma }\right)^T\ =)
^T\ P_{\sigma }^T\ N^T\ =\ \left(P_{\sigma }^T\ M^{-1}\right)^T\ P_{\sigma }^{-1}\ N^T\ =\)
^T\ P_{\sigma }\ P_{\sigma }^{-1}\ N^T\ =\ \left(M^{-1}\right)^T\ N^T)
§2f.
On considère la matrice^T\ N^T\) alors on vérifie
alors on vérifie 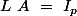
De plus la quantité de matrices différentes qui vérifient
différentes qui vérifient 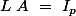 pour une matrice
pour une matrice  de rang
de rang 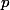 donnée est la quantitée d'ensembles de
donnée est la quantitée d'ensembles de 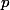 vecteurs colonne libres dans la matrice
vecteurs colonne libres dans la matrice 
Cas particulier:
Quand la matrice est carrée, la matrice
est carrée, la matrice  est unique
est unique
Démonstration:
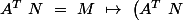^T\ =\ M^T\ \mapsto \ N^T\ A\ =\ M^T)
^T\ N^T\ A\ =\ I_p\ \mapsto \ L\ A\ =\ I_p)
Du résultat précédent on obtient qu'on ne peut avoir deux matrices différentes si on permute les colonnes de
différentes si on permute les colonnes de 
Il faut donc construire une autre matrice inversible à partir des colonnes de la matrice
à partir des colonnes de la matrice  et de telle sorte que la nouvelle matrice possède au moins une colonne différente que celles de
et de telle sorte que la nouvelle matrice possède au moins une colonne différente que celles de 
si des fois que ça tente quelqu'un de voir si j'ai fait des fautes...(mais bon ça saoule -...faut vraiment avoir envie de
"lire" )
-Matrices de
Préalablement pour
Éventuellement on écrira
Par conséquent
Formules élémentaires
Soit
§1.Matrices de permutation
Soit
Donc
Les coefficients de
Il n'y a qu'un seul
Les matrices de permutation d'ordre
À
Avec le symbole de Kronecker où
L'ensemble des matrices de permutation d'ordre
§1a.
On montre qu'une matrice de permutation est inversible
Son déterminant vaut la signature
Démonstration
Le calcul de la signature compte le nombre de permutations depuis l'ordre originel
De plus on montre que le déterminant d'une matrice de permutation vaut
Elle est donc inversible
Comme le déterminant du produit de deux matrices carrées est le produit des déterminants de ces deux matrices et comme les matrices de permutation d'ordre
§1b.
On montre que si
Démonstration
Évident puisque le groupe formé des matrices de permutation d'ordre
§1c.
On montre que l'inverse d'une matrice de permutation est sa transposée
Démonstration
Soit
et comme
§1d.
Le seul coefficient de valeur un de la colonne
Par exemple
Par conséquent
Soit
On montre que la
et la
Démonstration
Soit
À présent calculons
§1e.
Si
Démonstration
Évident selon
§2.Matrices de rang maximal
Soit
Donc
§2a.
On montre que l'on vérifie l'équivalence:
Démonstration:
D'une part on vérifie toujours l'implication
D'autre part comme
et on sait que toute matrice d'ordre
§2b.
On montre que l'on vérifie
Démonstration:
Supposons que
par conséquent
si on suppose que
mais le contexte est que
§2c.
On montre qu'il existe une matrice inversible
Démonstration:
il existe donc
§2d.
On se donne la matrice inversible
Au paragraphe précédent on a vu qu'une telle matrice existe
Et on se donne la matrice
On montre que l'on vérifie
Démonstration:
Notons
Cette notation très peu pratique est choisie malgré tout car
Donc en considérant le symbole de Kronecker on a l'égalité
Et notons
Là encore cette notation est à priori très peu pratique mais comme on va le voir elle ne sert juste qu'à dire que le coefficient
Selon
Par ailleurs
et on sait que toutes les colonnes de
on peut poser l'injection
de sorte que
et par conséquent
par ailleurs on vérifie aussi
On arrive donc à l'égalité à démontrer suivante:
par ailleurs comme
§2e.
Soit
Et posons la matrice
Et considérons la matrice
Alors on montre d'une part que
et d'autre part on vérifie l'égalité
Démonstration
Il est évident que la matrice de permutation permute les mêmes colonnes de
De sorte qu'en posant
§2f.
On considère la matrice
De plus la quantité de matrices
Cas particulier:
Quand la matrice
Démonstration:
Du résultat précédent on obtient qu'on ne peut avoir deux matrices
Il faut donc construire une autre matrice inversible
Re: np matrice de rang n ou p
...et le dernier sur ce sujet là du paragraphe 2 des matrices de rang maximal
autant placer le dernier et en fait je ne pensais pas être obligé de faire une démo pour ce résultat là : je trouvais ça évident mais bof ma démo est compliquée je trouve et je ne vois pas moyen de la faire plus simple
§2g.
\) et
et \) sont des matrices diagonales qui possèdent
sont des matrices diagonales qui possèdent 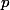 coefficients de valeur
coefficients de valeur  (tous les autres sont nuls)
(tous les autres sont nuls)
 et on vérifie les équivalences
et on vérifie les équivalences

Démonstration
\) et
et \)
par conséquent\) et
et \)
Ensuite on notera les coefficients de
les coefficients de 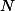 et
et  les coefficients de
les coefficients de 
par conséquent pour tout
pour tout  et
et 
Par ailleurs dans la démonstration du paragraphe §2d. on a vu qu'il existe une injection
telle que}\) pour tout
pour tout  et
et 
avec le symbole de Kronecker delta à indices décrit précédemment
par conséquent}\) pour tout
pour tout  et
et 
Effectuons le produit\) et notons $\ t_{ij}\ $ ses coefficients
et notons $\ t_{ij}\ $ ses coefficients
}\ \delta _{1,\varphi \left(j\right)}\ +\ \ldots \ +\ \delta _{n,\varphi \left(i\right)}\ \delta _{n,\varphi \left(j\right)})
de sorte qu'on obtient l'implication}\ \delta _{a,\varphi \left(j\right)}\ =\ \delta _{b,\varphi \left(i\right)}\ \delta _{b,\varphi \left(j\right)}\ =\ 1\ \Rightarrow \ a\ =\ b\ =\ \varphi \left(i\right)\ =\ \varphi \left(j\right))
de sorte aussi que la somme qui définie le coefficient se ramène à un seul terme
se ramène à un seul terme
}\ \delta _{a,\varphi \left(j\right)}\) avec
avec 
De plus}\ \delta _{k,\varphi \left(j\right)}\ =\ 1\ \Rightarrow \ k\ =\ \varphi \left(i\right)\ =\ \varphi \left(j\right))
et comme est injective et comme de plus il s'agit du symbole de Kronecker alors
est injective et comme de plus il s'agit du symbole de Kronecker alors 
et comme enfin ce coefficient appartient à une matrice carrée d'ordre
appartient à une matrice carrée d'ordre 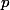
alors et
et  et donc
et donc 
À présent effectuons le produit\) et notons
et notons  ses coefficients
ses coefficients
}\ \delta _{j,\varphi \left(1\right)}\ +\ \ldots \ +\ \delta _{i,\varphi \left(p\right)}\ \delta _{j,\varphi \left(p\right)})
Pour que}\ \delta _{j,\varphi \left(a\right)}\ =\ \delta _{i,\varphi \left(b\right)}\ \delta _{j,\varphi \left(b\right)}\ =\ 1)
il faut que\ =\ \varphi \left(b\right)\) il faut déjà que
il faut déjà que  car
car  est injective
est injective
Si cette somme se ramène donc à un seul terme (qui si il n'est pas nul sera le seul terme non nul de la sommation
de sorte qu'on obtient l'implication
}\ \delta _{j,\varphi \left(a\right)}\ =\ 1\ \Rightarrow \ i\ =\ j\ =\ \varphi \left(a\right)) avec
avec  car
car  est d'ordre
est d'ordre 
on a donc\ =\ i\ =\ j)
il n'existe donc que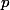 coefficients de valeur
coefficients de valeur  dans cette matrice et ils sont tous situés sur la diagonale
dans cette matrice et ils sont tous situés sur la diagonale
autant placer le dernier et en fait je ne pensais pas être obligé de faire une démo pour ce résultat là : je trouvais ça évident mais bof ma démo est compliquée je trouve et je ne vois pas moyen de la faire plus simple
§2g.
Démonstration
par conséquent
Ensuite on notera
par conséquent
Par ailleurs dans la démonstration du paragraphe §2d. on a vu qu'il existe une injection
telle que
avec le symbole de Kronecker delta à indices décrit précédemment
par conséquent
Effectuons le produit
de sorte qu'on obtient l'implication
de sorte aussi que la somme qui définie le coefficient
De plus
et comme
et comme enfin ce coefficient
alors
À présent effectuons le produit
Pour que
il faut que
Si cette somme se ramène donc à un seul terme (qui si il n'est pas nul sera le seul terme non nul de la sommation
de sorte qu'on obtient l'implication
on a donc
il n'existe donc que
Re: np matrice de rang n ou p
...et pour conclure: un exemple (histoire d'avoir un visuel)
 est de rang 4
est de rang 4
on peut construire (donc comme il est dit au §2c par exemple) la matrice inversible (non unique)

de cette matrice là on obtient (voir §2d)

et on vérifie toutes les formules des paragraphes §2e §2f §2g
ou alors (entre autre)
de cette matrice là on obtient

et on vérifiera les mêmes formules
sujet terminé
on peut construire (donc comme il est dit au §2c par exemple) la matrice inversible (non unique)
de cette matrice là on obtient (voir §2d)
et on vérifie toutes les formules des paragraphes §2e §2f §2g
ou alors (entre autre)
de cette matrice là on obtient
et on vérifiera les mêmes formules
sujet terminé
Re: np matrice de rang n ou p
...tiens à propos
^T\ N^T\ -\ I_n\right)\ =\ n\ -\ p)
la démo que j'ai fait tiens en trois lignes mais j'avoue que j'ai pas osé la faire tout de suite ...(j'ai juste dit dans mon lit que franchement il doit bien y avoir une astuce pour la faire et que ça fasse pas trente lignes et en fait il me fallait voir comment se comporte^T\ N^T) cette matrice quand on regarde
cette matrice quand on regarde 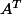
comme quoi des fois faut pas en faire une maladie mais j'étais dans mon lit en train de me dire que je suis con d'être là à dans mon lit à y penser mais à ne rien tenter
la démo que j'ai fait tiens en trois lignes mais j'avoue que j'ai pas osé la faire tout de suite ...(j'ai juste dit dans mon lit que franchement il doit bien y avoir une astuce pour la faire et que ça fasse pas trente lignes et en fait il me fallait voir comment se comporte
comme quoi des fois faut pas en faire une maladie mais j'étais dans mon lit en train de me dire que je suis con d'être là à dans mon lit à y penser mais à ne rien tenter
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
