Maths expliquer simplement

par **latinosbr** » 25 Mar 2010, 17:47

bonsoire à tous alors voila je suis actuellement entrain de suivre des cours de maths àl'université mais beaucoup de théorème et de notions sont expliquer de façon trop compliquer ; n'ayant une maturitée (bac) non scientifique (économique) je n'ai jamais vue ces notions pouriez vous silvoupler me les écxpliquer de la façons la plus simple posible avec si possible des exemples .

alors voila:
-les séries
-les suites
-les suites convergantes, Suites récurrentes
-le théorème des 2 gendarmes.
-continuité d'une limite (je vois pour 2 fonctions mais pour limites :-/ )
-un voisinage
-poles et polaires
-droites et points conjugés
-concrètement en exemple comment savoire si c'est un espace vectoriel et sous espace vectoriel.
-dépendance linéaire
-les générateurs
-les bases canonique
-l'algorytme de Gauss
-comment résoudre des équations sinus , cosinus (exemple racine carré de sinus; 2*cos(2x) ; dérivée des équation trigo (autre que sin x , cos x )
-Formules de bissection
-Conjugués harmoniques

je sais c'est beaucoup demander mais j'ai bo chercher dans les livres lire et relire les notes pas moyen de comprendre svp aider moi .

par **Dinozzo13** » 25 Mar 2010, 19:54

Salut !
Je vais te dire ce que je sais :+++:

Définition d'une suite : Soit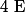

une partie non vide de

; on appelle suite réelle définie sur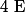

toutes fonction de

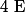dans

; l'image de

est notée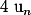

, à ne pas confondre avec la suite

.

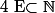tel que

Les suites convergentes : Soit

un réel et

une suite ; on dit que

converge vers

lorsque

converge vers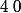

.

équivaut à

Suites définies par récurrence : Une suite (u_n) est dite récurrente si et seulement si elle est définie par son premier terme et le terme suivant du terme général.

ex : Soit la suite

définie par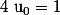

et pour tout entier

,

le théorème des gendarmes : Soient

et

trois suites. Dans ces conditions, si

et

converge vers un réel

et si à partir d'un certain rang on a :

alors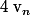

converge vers

.

et si à partir d'un certain entier

,

, alors :

équivaut à

donc

Quelque dérivées de fonctions trigonométriques :

On parle de voisinage lorsqu'on veux savoir ce qui se passe lorsqu'on se rapproche d'un nombre (précisé dans l'énoncé).
En ce qui concerne les pôles et polaires, je connais des choses sur les coordonnées polaires mais je ne sais pas si c'est ce que tu veux.
En espérant t'avoir aidé :++:

par **Nightmare** » 25 Mar 2010, 20:05

Je ne crois pas qu'on puisse faire mieux que tes profs ou tes bouquins. Peut être qu'on peut t'expliquer de manière détaillé un point précis du cours, mais pas tout un cours ! As-tu songé à un prof particulier?

par **latinosbr** » 26 Mar 2010, 08:32

merci dinnozo. je conte prendre des cours privé mais seulement après ce semestre car ce sont des cours intensifs donc pas vraiment le temps de prendre des cours privés; mais je souhaiterait juste essayer de comprendre le max pour revoire le temps par après avec un profs privé