Je ne vaut rien en écriture mathématique alors je n'aurai pas les belles représentations que les autres ont.
Je pense me faire comprendre tout de même. Alors la longueur d'arc de e^x entre 0 et 4.
J'intègre de 0 à 4: ;)(1+(e^x)^2)
Changement de variable e^x=tan(z)
J'arrive à ;)(1+tan^2(z)) ce qui est ;)(sec^2(z)) soit l'intégrale de sec(z) qui est ln|sec(z)+tan(z)|
Or je ne parvient pas à faire mon changement de borne et je viens de penser que j'ai oublié de changer dx en dz.
Un petit d'explication serait apprécié.
Merci
Longueur d'arc de [0, 4] de e^x
9 messages
- Page 1 sur 1
Salut,
Si e^x=tan(z) alors
1) x=ln(tan(z)) donc dx=tan'(z)/tan(z)dz=dz/(sin(z)cos(z))
2) z=arctan(e^x) donc lorsque x varie de 0 à 4, z varie de arctan(e^0)=pi/4 à arctan(e^4)
Et de chercher la primitive de (1+tan^2(z)) "tout seul", c'est à dire sans tenir compte du facteur supplémentaire lié au dx->dz ne sert à rien.
(1+tan^2(z)) "tout seul", c'est à dire sans tenir compte du facteur supplémentaire lié au dx->dz ne sert à rien.
P.S. Perso, je poserais plutôt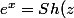=\frac{e^z-e^{-z}}{2}\) (sinus hyperbolique)
(sinus hyperbolique)
qui donne}=Ch(z)=\frac{e^z+e^{-z}}{2}) (cosinus hyperbolique)
(cosinus hyperbolique)
Si e^x=tan(z) alors
1) x=ln(tan(z)) donc dx=tan'(z)/tan(z)dz=dz/(sin(z)cos(z))
2) z=arctan(e^x) donc lorsque x varie de 0 à 4, z varie de arctan(e^0)=pi/4 à arctan(e^4)
Et de chercher la primitive de
P.S. Perso, je poserais plutôt
qui donne
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Salut,
Si e^x=tan(z) alors
1) x=ln(tan(z)) donc dx=tan'(z)/tan(z)dz=dz/(sin(z)cos(z))
2) z=arctan(e^x) donc lorsque x varie de 0 à 4, z varie de arctan(e^0)=pi/4 à arctan(e^4)
Et de chercher la primitive de (1+tan^2(z)) "tout seul", c'est à dire sans tenir compte du facteur supplémentaire lié au dx->dz ne sert à rien.
(1+tan^2(z)) "tout seul", c'est à dire sans tenir compte du facteur supplémentaire lié au dx->dz ne sert à rien.
P.S. Perso, je poserais plutôt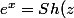=\frac{e^z-e^{-z}}{2}\) (sinus hyperbolique)
(sinus hyperbolique)
qui donne}=Ch(z)=\frac{e^z+e^{-z}}{2}) (cosinus hyperbolique)
(cosinus hyperbolique)
Si e^x=tan(z) alors
1) x=ln(tan(z)) donc dx=tan'(z)/tan(z)dz=dz/(sin(z)cos(z))
2) z=arctan(e^x) donc lorsque x varie de 0 à 4, z varie de arctan(e^0)=pi/4 à arctan(e^4)
Et de chercher la primitive de
P.S. Perso, je poserais plutôt
qui donne
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
