Limites, exp.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
RoRo57
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Déc 2011, 12:36
-
 par RoRo57 » 19 Déc 2011, 12:45
par RoRo57 » 19 Déc 2011, 12:45
Bonjour à tous !
J'ai aujourd'hui besoin de vous pour une formalité ... Mais qui m'ennuis !
En effet je n'arrive pas à trouver la bonne forme de la fonction pour déterminer cette limite ..

.. Ma calculette m'indique qu'elle vaut 0 mais je vois pas comment arranger ça ! La factorisation mène nul part et je ne vois pas de changement de variable ...
Cette limite est l'inverse d'une limite remarquable sauf qu'on a

et non
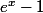
... Bref je memmêle les pinceaux !
Voilà, merci d'avance !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Déc 2011, 12:49
par Nightmare » 19 Déc 2011, 12:49
Salut,
quelle(s) factorisation as-tu essayé?
A priori, c'est l'exponentielle qui l'emporte sur les autres termes, il pourrait donc être judicieux de factoriser par cette dernière.
-
RoRo57
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Déc 2011, 12:36
-
 par RoRo57 » 19 Déc 2011, 13:35
par RoRo57 » 19 Déc 2011, 13:35
Nightmare a écrit:Salut,
quelle(s) factorisation as-tu essayé?
A priori, c'est l'exponentielle qui l'emporte sur les autres termes, il pourrait donc être judicieux de factoriser par cette dernière.
Eh bien justement par l'exp :s
J'obtiens

Ça ressemble à une autre limite remarquable sauf qu'elle s'utilise pour
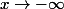
...
Cependant c'est elle que je dois utiliser ? En posant un truc du style X = -x ?
Merci Nightmare.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Déc 2011, 13:44
par Nightmare » 19 Déc 2011, 13:44
N'as-tu pas dans ton cours la limite
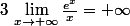
?
-
RoRo57
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Déc 2011, 12:36
-
 par RoRo57 » 19 Déc 2011, 13:51
par RoRo57 » 19 Déc 2011, 13:51
Nightmare a écrit:N'as-tu pas dans ton cours la limite
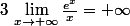
?
Si bien sûr mais c'est l'inverse que j'ai dans ma fonction :hein:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 19 Déc 2011, 13:54
par Nightmare » 19 Déc 2011, 13:54
RoRo57 a écrit:Si bien sûr mais c'est l'inverse que j'ai dans ma fonction :hein:
Et? N'a-t-on rien qui nous donne la limite de l'inverse?
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 19 Déc 2011, 13:54
par vincentroumezy » 19 Déc 2011, 13:54
Oui, mais la limite de l'inverse, c'est linverse de la limite.
Edit:grillé.
-
RoRo57
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Déc 2011, 12:36
-
 par RoRo57 » 19 Déc 2011, 13:56
par RoRo57 » 19 Déc 2011, 13:56
RoRo57 a écrit:Si bien sûr mais c'est l'inverse que j'ai dans ma fonction :hein:
Ah mais il faut simplement factoriser par x et se retrouver avec un "

"
Si oui ... Bien je m'excuse pour la gêne occasionnée ...
Cependant si tu voulais me faire comprendre une autre méthode peux-tu me l'expliciter ?
Merci
EDIT: Oui donc l'inverse de l'infini est bien 0 ...
Merci pour la démarche, je n'y avais pas pensé !
-
vincentroumezy
- Membre Irrationnel
- Messages: 1363
- Enregistré le: 19 Juil 2010, 11:00
-
 par vincentroumezy » 19 Déc 2011, 14:37
par vincentroumezy » 19 Déc 2011, 14:37
RoRo57 a écrit:Ah mais il faut simplement factoriser par x et se retrouver avec un "

"
Si oui ... Bien je m'excuse pour la gêne occasionnée ...
Cependant si tu voulais me faire comprendre une autre méthode peux-tu me l'expliciter ?
Merci
EDIT: Oui donc l'inverse de l'infini est bien 0 ...
Merci pour la démarche, je n'y avais pas pensé !
C'est la bonne réponse (évite justed'écrire 1/(l'infini), car l'infini n'est pas un réel)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 147 invités
