Limite d une suite

[marc2015]

salut
j ai un exercice sur les limites d une suite réel
je n arrive pas a répondre a la deuxième question ii)
si possible de me donner une réponse

exercice
1) soit a un réel et (un) la suite définie pour tout entier non nul n par un=(cos(pi.a))^2n

i) Déterminer la limite de un lorsque a est un entier .
ii)Déterminer la limite de un lorsque a n 'est pas un entier.

ma réponse
i) cos pi a = (-1)^a
deux cas a discuter
1er cas si a =2q (pair) d ou cos pi a = +1 alors un= 1^2n =1
2em cas si a=2q+1 d ou cos pi a = -1 alors un=(- 1)^2n =1

dans les deux cas lim un =1

ii) Déterminer la limite de un lorsque a n 'est pas un entier ??

si a n 'est pas un entier donc a est un rationnel on pose a=p/q avec q non nul
un=(cos(pi.p/q))^2n

je n arrive pas transformer cos(pi.p/q)

merci

[capitaine nuggets]

Salut !

C'est faux, si n'est pas entier, c'est que appartient à . peut très bien être irrationnel (pense à par exemple).

As-tu essayé de mettre sous la forme ?

[marc2015]

salut capitaine nuggets

c est dans la partie suite géométrique et applications
sans utiliser l exponentiel

merci

[capitaine nuggets]

Essaye d'étudier le quotient 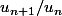(sous réserve que soit non nul !)

[marc2015]

salut capitaine nuggets
svp en cherche une limite de la suite dans le cas ou a n est pas un entier
pourquoi calculer le quotient u_{n+1}/u_n

merci

[bolza]

Bonjour,

as-tu remarquer que cos(pi.a) ne dépend pas de n, et est donc constant (par rapport à n) ?
si tu nomme cette constante k qu'est-ce que te donne la suite un ?

Ensuite le fait que k soit un cosinus ça devrait te donner des information sur cette constante
qui devrait te permettre de conclure.

[marc2015]

Bonjour bolza

1) soit a un réel et (un) la suite définie pour tout entier non nul n par un=(cos(pi.a))^2n

i) Déterminer la limite de un lorsque a est un entier .
ii)Déterminer la limite de un lorsque a n 'est pas un entier.


non je n est pas remarqué que cos(pi.a) ne dépend pas de n, et est donc constant (par rapport à n) ?
si on pose k=cos(pi.a) et -1<=cos(pi.a)<=1 don c -1<=k<=1 donc o<=k²<=1 on pose
un=k^2n

on pose q=k² d ou 0<=q<=1 trois cas q=0 ou q=1 ou 0< q<1 donc lim un = o ou lim un=1

mon problème c est comment repondre aux qux question suivant la nature de a ( entier et non entier )
svp je n est pas compris les cas a étudier sur a (lorsque a est un entier et lorsque a n 'est pas un entier )

si possible de me donner une réponse

merci

[bolza]

on pose q=k² d ou 0<=q<=1 trois cas q=0 ou q=1 ou 0< q<1 donc lim un = o ou lim un=1

Oui c'est exactement ça, maintenant si tu te rappelle que q = (cos(pi.a))² :
-pour quels valeurs de a avons nous q = 0 ?
-pour quels valeurs de a avons nous q = 1 ?
-pour quels valeurs de a avons nous 0 < q < 1 ?

[marc2015]

salut bolza
merci beaucoup pour votre soutien ( restons en contact svp)

On pose q = (cos(pi.a))² :
-pour a =(k/2)+1 (k entier) nous avons q = 0 ( ici je ne suis pas sur ) a appartient à Q
-pour a=0 ou 1 ou 2 donc a entier ( a appartient à Z) nous avons q = 1
-pour a appartient à R/Z avons nous 0 < q < 1

merci

[bolza]

-pour a =(k/2)+1 (k entier) nous avons q = 0 ( ici je ne suis pas sur ) a appartient à Q

non pas tout à fait, regardez le cercle trigonométrique, cos(pi/2) = 0 (là vous êtes en haut du cercle)
ensuite à chaque fois que vous faite un demi-tour du cercle, le cos est égal à 0.
Et faire un "demi-tour" c'est ajouter pi, donc c'est cos(pi/2+ k.pi) qui est égal à 0, pas cos(k.pi/2 + pi)
(en fait cos(k.pi/2+p) est égal à 0 seulement pour k impair).

( ici je ne suis pas sur ) a appartient à Q

mis à part la rectification ci-dessus, que dire de k/2 si k est pair ?

-pour a=0 ou 1 ou 2 donc a entier ( a appartient à Z) nous avons q = 1
-pour a appartient à R/Z avons nous 0 < q < 1
merci

Oui, enfin presque pour le dernier point , il ne faut pas non plus que a soit de la forme trouvé
dans le cas q=0.

[marc2015]

salut bolza
merci pour votre message
On pose q = (cos(pi.a))² :

-pour a =k+(1/2) (k entier) nous avons q = 0
-pour a entier et a différent k+(1/2) ( a appartient à Z) nous avons q = 1
-pour a appartient à R/Z et a différent k+(1/2) (k entier) avons nous 0 < q < 1

svp i) Déterminer la limite de un lorsque a est un entier .

pour a entier et a différent k+(1/2) ( a appartient à Z) nous avons q = 1
lim un=1

ii)Déterminer la limite de un lorsque a n 'est pas un entier.

on deux sous cas

1)pour a =k+(1/2) (k entier) nous avons q = 0


lim un=0

2)pour a appartient à R/Z et a différent k+(1/2) (k entier) avons nous 0 < q < 1
lim un=0

si possible de vérifier ma réponse
merci

[bolza]

salut bolza
merci pour votre message
On pose q = (cos(pi.a))² :

-pour a =k+(1/2) (k entier) nous avons q = 0
-pour a entier et a différent k+(1/2) ( a appartient à Z) nous avons q = 1
-pour a appartient à R/Z et a différent k+(1/2) (k entier) avons nous 0 < q < 1

svp i) Déterminer la limite de un lorsque a est un entier .

pour a entier et a différent k+(1/2) ( a appartient à Z) nous avons q = 1
lim un=1

ii)Déterminer la limite de un lorsque a n 'est pas un entier.

on deux sous cas

1)pour a =k+(1/2) (k entier) nous avons q = 0


lim un=0

2)pour a appartient à R/Z et a différent k+(1/2) (k entier) avons nous 0 < q < 1
lim un=0

si possible de vérifier ma réponse
merci

Oui :++: , mais est-ce que k+(1/2) peut être entier si k est entier ?

[marc2015]

salut bolza
merci beaucoup
c est la première fois que je rencontre un professeur de maths qui a une méthode très efficace et qui aide l élève a trouver seul la réponse
vous demandez des questions qui enlèvent tous ce qui n est pas claire dans l esprit
le problème c est au niveau de la compréhension du cours .



k+(1/2) ne peut pas être entier si k est entier

merci

[bolza]

salut bolza
merci beaucoup
c est la première fois que je rencontre un professeur de maths qui a une méthode très efficace et qui aide l élève a trouver seul la réponse
vous demandez des questions qui enlèvent tous ce qui n est pas claire dans l esprit
le problème c est au niveau de la compréhension du cours .



k+(1/2) ne peut pas être entier si k est entier

merci

Heuu merci ^^ mais je ne suis pas un professeur de math ^^
Je viens de relire un peu le fil et il y a un truc auquel je n'ai pas fait attention :
Tu distingue le cas q = 0 et 0 < q < 1, et tu trouve le même résultat dans les deux cas,
tu peux je pense directement unifier ces deux cas :lol3:

[marc2015]

salut bolza
merci pour votre soutien
comment unifier les deux cas

merci

[bolza]

???

au lieu de distinguer le distinguer trois cas (q= 1, q= 0 et 0 < q < 1)
tu distingue que deux cas, q= 1 et 0 <= q < 1, le raisonnement reste le même