Limite
14 messages
- Page 1 sur 1
limite
rebonjour a tous,voici un exercice qui me semble pas si dur que ca mais j'ai tt de même des difficulté,pouvez vous m'aidez svp.merci
determiner les réels a, b ,c de facon que la courbe representative de la fonction f définie sur R\{-c} par f(x)= (ax+b)/(x+c) passe par les points A(-1;6) et B(4.1) et admette la droite d'equation y=2 pour asymptote.
donc voila l'exercice.
merci bien
determiner les réels a, b ,c de facon que la courbe representative de la fonction f définie sur R\{-c} par f(x)= (ax+b)/(x+c) passe par les points A(-1;6) et B(4.1) et admette la droite d'equation y=2 pour asymptote.
donc voila l'exercice.
merci bien
re
salut,euh oui c'est bien y=2.
euh purrace,comment on sait alors que y nous aide a en deduire que a=2
euh purrace,comment on sait alors que y nous aide a en deduire que a=2
Re,
on a=\frac{ax+b}{x+c})
ta courbe passe par le point A (-1,6) donc les coordonnées de A verifient l'equation de f soit f(-1)=6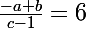 (1)
(1)
de même ta courbe passe par le point B(4,1) donc idem on a f(4)=1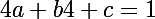 (2)
(2)
de plus on te dit que la courbe representative de la fonction f admette la droite d'equation y=2 pour asymptote donc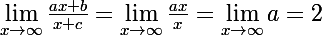
donc a=2
Rappel :en +inf et -inf, une fct rationnelle a même limite que le quotient de ses termes de + haut degrè
je vais refaire mes calculs pour voir
tu connais a=2 sert toi de (1) et (2)
on a
ta courbe passe par le point A (-1,6) donc les coordonnées de A verifient l'equation de f soit f(-1)=6
de même ta courbe passe par le point B(4,1) donc idem on a f(4)=1
de plus on te dit que la courbe representative de la fonction f admette la droite d'equation y=2 pour asymptote donc
donc a=2
Rappel :en +inf et -inf, une fct rationnelle a même limite que le quotient de ses termes de + haut degrè
je vais refaire mes calculs pour voir
tu connais a=2 sert toi de (1) et (2)
re
merci beaucoup,j'ai trouver comme toi a propos de(1) et(2) mais je n'arrive pas a trouver b et c.par hasard,il n'y a pas un rapport avec des equation ou qqch dans le genre????
re
ah ca m'enerve,je n'y arrive pas dutout,je ne sais même plus comment il faut faire,pouvez vous m'expliquer comment il faut faut faire mais sans me donner la reponse.merci d'avance
fonfon a écrit:oui ,il faut resoudre (1) et (2)
ta courbe passe par le point A (-1,6) donc les coordonnées de A verifient l'equation de f soit f(-1)=6(1)
de même ta courbe passe par le point B(4,1) donc idem on a f(4)=1(2)
et que a=2 donc
(1)
(2)
il faut que tu remplaces a par 2 et que tu resous le systeme...
(1)
(2)
donc ici b=... et c=...
re
ah voila merci,je crois que j'ai trouver,c=0 donc b=-4
voila,bon ben il ne me reste plus qu'a vous remercier de votre aide.
voila,bon ben il ne me reste plus qu'a vous remercier de votre aide.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
