Limite ts

par **Rom59math** » 04 Oct 2016, 18:19

Soient la fonction f définie sur r par :
F(x)=x/2-sin(x)
1) établir que pour tout x>0:
0<x/3<x/2-sinx<x
2)déduire lim f(x)?
3)x<0:
0>x/3>x/2-sinx>x
4) déduire lim f(x)

par **chan79** » 04 Oct 2016, 18:33

Bonsoir
Revois l'énoncé.
Pour x=pi/2, ça ne marche pas au 1.

par **Rom59math** » 04 Oct 2016, 18:54

Nan l'énoncé est bon

par **chan79** » 04 Oct 2016, 19:47

alors, il manque des parenthèses ... ?

par **Rom59math** » 04 Oct 2016, 19:50

Bah non

par **chan79** » 04 Oct 2016, 19:52

Rom59math a écrit:1) établir que pour tout x>0:
0<x/3<x/2-sinx<x

si tu remplaces x par pi/2 ça fait

0<pi/6<-0.21...

par **Rom59math** » 04 Oct 2016, 19:56

PK tu remplace x par pi/2

par **samoufar** » 04 Oct 2016, 20:26

Bonsoir,

À ma connaissance

, donc pour être vraie ton inégalité doit marcher pour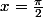

, ce qui n'est pas le cas...

Limite ts

Limite ts

Re: Limite ts

Re: Limite ts

Re: Limite ts

Re: Limite ts

Re: Limite ts

Re: Limite ts

Re: Limite ts

Qui est en ligne