Limite difficile par niveau de terminal
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 07 Mar 2015, 11:19
par adamNIDO » 07 Mar 2015, 11:19
Bonjour,
comment je peux resoudre cette limite sans utilise l'hopital ou bien DL dordre 2 au V=0 seulement par niveau de terminal
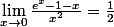
merci
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 07 Mar 2015, 12:00
par nodjim » 07 Mar 2015, 12:00
As tu regardé ce que ça donne avec la dérivée ?
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 07 Mar 2015, 12:11
par adamNIDO » 07 Mar 2015, 12:11
nodjim a écrit:As tu regardé ce que ça donne avec la dérivée ?
comment ca j'ai pas compris votre methode
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 07 Mar 2015, 12:41
par nodjim » 07 Mar 2015, 12:41
En comparant les pentes du numérateur et du dénominateur aux abords de 0, tu devrais pouvoir conclure.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 07 Mar 2015, 13:08
par adamNIDO » 07 Mar 2015, 13:08
nodjim a écrit:En comparant les pentes du numérateur et du dénominateur aux abords de 0, tu devrais pouvoir conclure.
pouvez vous decrire votre methode
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 07 Mar 2015, 13:23
par nodjim » 07 Mar 2015, 13:23
Pour moi la fonction f1: e^x-1-x a pour limite 0 en 0. Sa dérivée a pour pente 1 aux abords de 0.
La fonction f2: x² a pour limite 0 en 0, sa dérivée est 2x, sa pente est 2.
f1/f2 aux abords de zéro vaut 1/2.
Je ne sais pas si c'est admis en Terminale, ça fait bien longtemps que je ne suis plus au courant du programme.
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 07 Mar 2015, 13:39
par adamNIDO » 07 Mar 2015, 13:39
nodjim a écrit:Pour moi la fonction f1: e^x-1-x a pour limite 0 en 0. Sa dérivée a pour pente 1 aux abords de 0.
La fonction f2: x² a pour limite 0 en 0, sa dérivée est 2x, sa pente est 2.
f1/f2 aux abords de zéro vaut 1/2.
Je ne sais pas si c'est admis en Terminale, ça fait bien longtemps que je ne suis plus au courant du programme.
merci beaucoup moi aussi je sais pas sil est admis en terminale ou non
s'appelle comment cette methode

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 07 Mar 2015, 14:25
par zygomatique » 07 Mar 2015, 14:25
nodjim a écrit:Pour moi la fonction f1: e^x-1-x a pour limite 0 en 0. Sa dérivée a pour pente 1 aux abords de 0.
La fonction f2: x² a pour limite 0 en 0, sa dérivée est 2x, sa pente est 2.
f1/f2 aux abords de zéro vaut 1/2.
Je ne sais pas si c'est admis en Terminale, ça fait bien longtemps que je ne suis plus au courant du programme.
sa pente est 2 ... en 1 ... mais en 0 ?
on en peux pas prendre la pente du numérateur en 0 et celle du numérateur en 1 ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 07 Mar 2015, 16:21
par Joker62 » 07 Mar 2015, 16:21
Hello,
Dans la mode des nouveaux programmes, on va sur le logiciel xCas et on tape :
f(x) := (exp(x)-1-x)/x^2
limite(f(x),x,0)
Sinon
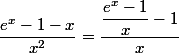
Si on pose
 = \dfrac{e^x-1}{x})
si
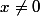
et
 = 1)
La limite recherchée est le taux d'accroissement de g en 0.
On prend géogébra et on lit la pente du coefficient directeur de la tangente en 0.
(C'est dans l'esprit du programme)
Sinon, ça se fait avec l'aide du théorème des gendarmes et d'inégalités fournies du type :
e^x > 1 + x + x^2/2 + x^3+6
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités