Intervalle de confiance à un niveau de confiance de 98 %
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Madodo
- Messages: 2
- Enregistré le: 18 Mar 2020, 10:01
-
 par Madodo » 25 Mar 2020, 12:04
par Madodo » 25 Mar 2020, 12:04
Bonjour,
Je suis en terminale es et on étudie en ce moment les intervalles de confiance à 95 % de niveau de confiance avec cette formule :
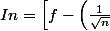; f+\left(\frac{1}{\sqrt{n}} \right) \right])
Mais j'aimerais savoir si il y a une possibilité avec une autre formule d'établir un intervalle de confiance à 98 % de confiance. Je ne le trouve nul part dans mes cours. J'ai trouvé la réponse avec les intervalles de fluctuations mais je n'y arrive pas avec les intervalles de confiance.
Merci beaucoup d'avance
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 25 Mar 2020, 20:53
par LB2 » 25 Mar 2020, 20:53
Bonjour Madodo,
Ta formule pour l'intervalle de confiance à 95% n'est pas bonne
C'est
}}{\sqrt{n}};f + \frac{1.96 \times \sqrt{f(1-f)}}{\sqrt{n}}])
Cette formule est introduite en seconde sous la forme simplifiée

Ce fameux 1.96 dépend du niveau de confiance de 95%.
Pour un niveau de confiance de 98%, il faut remplacer 1.96 par 2.33
Ces valeurs de 1.96 et de 2.33 sont les quantiles d'une loi de probabilité qui s'appelle la loi normale centrée réduite ou loi gaussienne.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
