Bonjour,
j'ai besoin d'aide pour cette intégral:
l'intégral de 0 à ln2 de 1/racinecarré(exp(x)+1)
Merci
Intergral
11 messages
- Page 1 sur 1
Je ne sais pas dans quelle classe tu es mais tu n'échapperas pas aux fonctions hyperboliques pour calculer cette intégrale, donc je te fais un résumé rapide.
sinh(x)=(e^x-e^-x)/2.
cosh(x)=(e^x+e^-x)/2; le terme hyperbolique provient du fait que le point M(cosh(x); sinh(x)) se promène sur une hyperbole, alors que le point N(cos(x); sin(x)), lui se balade sur le cercle trigonométrique.
Je te laisse étudier ces 2 fonctions qui sont inversibles sur R+;
La fonction tanh(x) est définie naturellement par tanh(x)=sinh(x)/cosh(x)=(e^x-e^-x)/(e^x+e^-x);
je te laisse le soin de vérifier que tanh est strictement croissante sur R à valeurs dans)-1; 1(, donc est inversible de )-1; 1( dans R; la fonction inverse est notée argtanh (lire argument de tangente hyperbolique); on trouve l'expression de argtanh en résolvant (e^x-e^-x)/(e^x+e^-x)=y <->
e^x(1-y)=e^-x(1+y)<->e^2x=(1+y)/(1-y)<-> x=(1/2)ln((1+y)/(1-y)); donc, argtanh(t)=
0,5ln((1+t)/(1-t)) et sa dérivée vaut (t)=0,5(1/(1+t)+1/(1-t))=0,5(2/(1-t²))=1/(1-t²);
; En fait on n'a pas du tout besoin de argtanh, car 1/(1-t²)=(1/2)(1/(1+t)+1/(1-t) et ln suffit!
C'était en fait pour te renseigner sur argtanh; pour ton intégrale, par contre,il faut que tu fasses t=V(e^x+1).
Par contre, la fonction arctan(x) dont la dérivée est 1/(1+x²) est indispensable pour intégrer les fonctions rationnelles.
sinh(x)=(e^x-e^-x)/2.
cosh(x)=(e^x+e^-x)/2; le terme hyperbolique provient du fait que le point M(cosh(x); sinh(x)) se promène sur une hyperbole, alors que le point N(cos(x); sin(x)), lui se balade sur le cercle trigonométrique.
Je te laisse étudier ces 2 fonctions qui sont inversibles sur R+;
La fonction tanh(x) est définie naturellement par tanh(x)=sinh(x)/cosh(x)=(e^x-e^-x)/(e^x+e^-x);
je te laisse le soin de vérifier que tanh est strictement croissante sur R à valeurs dans)-1; 1(, donc est inversible de )-1; 1( dans R; la fonction inverse est notée argtanh (lire argument de tangente hyperbolique); on trouve l'expression de argtanh en résolvant (e^x-e^-x)/(e^x+e^-x)=y <->
e^x(1-y)=e^-x(1+y)<->e^2x=(1+y)/(1-y)<-> x=(1/2)ln((1+y)/(1-y)); donc, argtanh(t)=
0,5ln((1+t)/(1-t)) et sa dérivée vaut (t)=0,5(1/(1+t)+1/(1-t))=0,5(2/(1-t²))=1/(1-t²);
; En fait on n'a pas du tout besoin de argtanh, car 1/(1-t²)=(1/2)(1/(1+t)+1/(1-t) et ln suffit!
C'était en fait pour te renseigner sur argtanh; pour ton intégrale, par contre,il faut que tu fasses t=V(e^x+1).
Par contre, la fonction arctan(x) dont la dérivée est 1/(1+x²) est indispensable pour intégrer les fonctions rationnelles.
Je sais pas non plus dans quelle classe tu est, mais tu n'as absolument pas besoin de fonctions hyperbolique pour résoudre le problème (mais de changement de variable...)
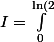}\frac{dx}{\sqrt{\exp(x)+1})
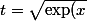+1}\ \Rightarrow\ \exp(x)=t^2-1\ \Rightarrow\ x=\ln(t^2-1)\ \Rightarrow\ dx=\frac{2t}{t^2-1}dt)
dt=\Big[\ln(t-1)-\ln(t+1)\Big]_{\sqrt{2}}^{\sqrt{3}}=\cdots)
Après, sans connaitre les changement de variables, ben je vois qu'une seule méthode :
Tu "tire d'un chapeau" la fonction=\ln\big(\sqrt{\exp(x)+1}-1 \big)-\ln\big(\sqrt{\exp(x)+1}+1 \big)\) , tu la dérive et...oh, miracle, la dérivée, c'est la fonction à intégrer...
, tu la dérive et...oh, miracle, la dérivée, c'est la fonction à intégrer...
Après, sans connaitre les changement de variables, ben je vois qu'une seule méthode :
Tu "tire d'un chapeau" la fonction
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
La fonction F(x)=ln(V(e^x+1)-1)-ln(V(e^x+1)+1) ne sort pas d'un chapeau, mais s'obtient avec le même changement de variable en calculant par exemple int(0; x)(1/V(e^u+1)du. Donc, si on ne connait pas le changement de variable, je ne vois pas comment on peut deviner que F est une primitive. Sinon, la fonction argtanh est totalement inutile pour le calcul d'une intégrale, mais puisqu'on en a parlé, on peut préciser ce que c'est.
J'aurais bien aimé savoir si cet exercice a été donné dans une classe ou s'il a été pêché ailleurs.
J'aurais bien aimé savoir si cet exercice a été donné dans une classe ou s'il a été pêché ailleurs.
Je soupçonnerait bien qu'en fait, c'est la dernière question d'un exo. où, auparavant, on t'a fait comme par hasard étudier et en particulier dériver d'une fonction ressemblant fortement à la fonction F ça dessus....paquito a écrit:...J'aurais bien aimé savoir si cet exercice a été donné dans une classe ou s'il a été pêché ailleurs.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Je soupçonnerait bien qu'en fait, c'est la dernière question d'un exo. où, auparavant, on t'a fait comme par hasard étudier et en particulier dériver d'une fonction ressemblant fortement à la fonction F ça dessus....
C'est bien possible; et s'il y a eu une erreur dans le calcul de F'(x), on comprend le problème qui s'est posé!
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
