Integrale très spéciale
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 23 Aoû 2009, 11:41
par cookiie » 23 Aoû 2009, 11:41
Bonjour! Je te prie d'aller d'urgence consulter le réglementVoici une integrale avec une répétition de formule si je ne me trompe pas?

transformation de l'expression :

Je pose U =

U' =

V =

V' =

Donc on applique la formule ..


Et puis il faudrait refaire la méthode U V .. avec l'integrale mais je suis P E R D U ca fait depuis 12h30 que je suis sur cette équation :--:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Aoû 2009, 11:49
par girdav » 23 Aoû 2009, 11:49
Tu peux y aller directement:
e^xdx = \fr 12 \sin\(2x\)e^x - \int \fr12 \sin\(2x\)e^xdx)
et dans la deuxième intégrale tu poses
 = \sin\(2x\))
et
 = e^x)
.
EDIT j'ai mis le

. C'est plus correct comme ça.
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 23 Aoû 2009, 12:06
par cookiie » 23 Aoû 2009, 12:06
girdav a écrit:Tu peux y aller directement:
e^xdx = \fr 12 \sin\(2x\) - \int \fr12 \sin\(2x\)e^xdx)
et dans la deuxième intégrale tu poses
 = \sin\(2x\))
et
 = e^x)
.
merci mais alors pour :
 - \int \fr12 \sin\(2x\)e^xdx)
Quel est le raport entre
 et cos2x)
?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Aoû 2009, 12:07
par girdav » 23 Aoû 2009, 12:07
cookiie a écrit:merci mais alors pour :
 - \int \fr12 \sin\(2x\)e^xdx)
Quel est le raport entre
 et cos2x)
?
La dérivée de
)
est
)
.
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 23 Aoû 2009, 12:20
par cookiie » 23 Aoû 2009, 12:20
girdav a écrit:La dérivée de
)
est
)
.
Ah oké .. mon dieu fallais le savoir, j'ai pas vu une formule qui m'aide à obtenir cette dérivée
-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 23 Aoû 2009, 12:52
par muse » 23 Aoû 2009, 12:52
Tu as fait une intergration par partie. Il manque pas un truc la ? 'est 1/2 sin(2x)*exp(x)- int...
-
mathelot
 par mathelot » 23 Aoû 2009, 13:11
par mathelot » 23 Aoû 2009, 13:11
cookiie a écrit:
transformation de l'expression :

possède une distance.
On peut donc dériver une fonction
de

dans

=f(x)+i g(x))
composante par composante
=f'(x)+i g'(x))
et aussi intégrer composante par composante
d'où
)
est la partie réelle de
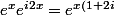})
une primitive de
dx)
est donc la partie réelle d'une primitive de
}dx)
d'où la partie réelle de
})
en primitivant l'exponentielle

en

qui vaut
)
+\frac{2}{5} sin(2x) \right))
car
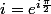
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 24 Aoû 2009, 10:36
par cookiie » 24 Aoû 2009, 10:36
muse a écrit:Tu as fait une intergration par partie. Il manque pas un truc la ? 'est 1/2 sin(2x)*exp(x)- int...
Si muse il manque l'exp' avant de soustraire l'integrale

-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 24 Aoû 2009, 10:38
par cookiie » 24 Aoû 2009, 10:38
mathelot a écrit:
possède une distance.
On peut donc dériver une fonction
de

dans

=f(x)+i g(x))
composante par composante
=f'(x)+i g'(x))
et aussi intégrer composante par composante
d'où
)
est la partie réelle de
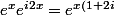})
une primitive de
dx)
est donc la partie réelle d'une primitive de
}dx)
d'où la partie réelle de
})
en primitivant l'exponentielle

en

qui vaut
)
+\frac{2}{5} sin(2x) \right))
car
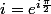
Ouh .. je pense que c'est pas encore de mon niveau tout ca

-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2009, 10:42
par girdav » 24 Aoû 2009, 10:42
cookiie a écrit:Si muse il manque l'exp' avant de soustraire l'integrale

J'ai finalement corrigé cette erreur. Merci à vous deux!
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 24 Aoû 2009, 11:03
par cookiie » 24 Aoû 2009, 11:03
girdav a écrit:J'ai finalement corrigé cette erreur. Merci à vous deux!
Merci à toi de participer ! :we:
Ceci dit cela ne me semble pas très juste quand même, je m'explique :
Si la dérivée de

est

Et que

reste

Pourquoi tu trouve cette expression
e^xdx = \fr 12 \sin\(2x\)e^x - \int \fr12 \sin\(2x\)e^xdx)
et non pas celle ci
e^xdx = \int \cos\(2x\)e^x - \int \fr12 \sin\(2x\)e^xdx)
Car la formule dit que :
U V - \int U' Ven sachant que :
V & V' =

U =

U' = \fr12 \sin\(2x\)
?
MODIFU & U' =

V = \fr12 \sin\(2x\)
V' =

Donc Ok tout va bien pour le moment :we: :we:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2009, 11:09
par girdav » 24 Aoû 2009, 11:09
On doit avoir
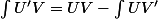
d'après la formule de dérivation d'un produit donc en prenant
 = V'(x) =e^x)
et
 = \cos(2x))
on trouve bien ce qu'il faut.
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 24 Aoû 2009, 11:54
par cookiie » 24 Aoû 2009, 11:54
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 24 Aoû 2009, 12:04
par girdav » 24 Aoû 2009, 12:04
Je crois qu'il y a un problème au niveau des parenthèses dans la première ligne, et dans la deuxième une exponentielle est mal placée.
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 24 Aoû 2009, 12:15
par cookiie » 24 Aoû 2009, 12:15
girdav a écrit:Je crois qu'il y a un problème au niveau des parenthèses dans la première ligne, et dans la deuxième une exponentielle est mal placée.
En effet, merci !
Par contre les exponentielles il y en a 3 et j'ai juste regroupé les deux avant l'integrale, je ne vois pas le mal :hein:
Modif !Maintenant je vois ! bah la faute de débutant :--:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
 transformation de l'expression :
transformation de l'expression :






