Inéquation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Kiwiks
- Membre Naturel
- Messages: 49
- Enregistré le: 30 Oct 2006, 19:50
-
 par Kiwiks » 30 Oct 2006, 19:52
par Kiwiks » 30 Oct 2006, 19:52
Bonjour, je bloque sur un exercice de maths, le voici :
Soit x un nombre réel quelconque.
a) Démontrer l'inégalité : x²-1 >= 2(x-1)
b)En déduire l'inégalité : x^4-1 >= 4(x-1)
Alors moi j'ai mis pour a) : x²-1-2x+2 >= 0
x²-2x+1 >= 0
(x-1)² >= 0
Puisqu'un carré est tjs positif alors cette inégalité est vérifiée.
Par contre pour le b) je n'y arrive pas du tout.
Merci beaucoup d'avance.
-
matteo182
- Membre Relatif
- Messages: 279
- Enregistré le: 01 Mai 2005, 01:14
-
 par matteo182 » 30 Oct 2006, 22:09
par matteo182 » 30 Oct 2006, 22:09
Salut,
Remarque que :
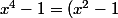(x^2 + 1))
et utilises a.
-
Kiwiks
- Membre Naturel
- Messages: 49
- Enregistré le: 30 Oct 2006, 19:50
-
 par Kiwiks » 01 Nov 2006, 15:37
par Kiwiks » 01 Nov 2006, 15:37
matteo182 a écrit:Salut,
Remarque que :
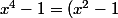(x^2 + 1))
et utilises a.
Donc en fait (x²-1)(x²+1) >= 2.2(x-1)
Je pense qu'il faut prouver que (x²+1) >= 2
alors je fait x²+1-2 >= 0
x²-1>=0
Mais là ce n'est pas toujours vrai que x²-1 >=0
Merci ...
-
Kiwiks
- Membre Naturel
- Messages: 49
- Enregistré le: 30 Oct 2006, 19:50
-
 par Kiwiks » 01 Nov 2006, 17:06
par Kiwiks » 01 Nov 2006, 17:06
matteo182 a écrit:Salut,
Remarque que :
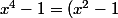(x^2 + 1))
et utilises a.
Donc en fait (x²-1)(x²+1) >= 2.2(x-1)
Je pense qu'il faut prouver que (x²+1) >= 2
alors je fait x²+1-2 >= 0
x²-1>=0
Mais là ce n'est pas toujours vrai que x²-1 >=0
Merci ...
-
Kiwiks
- Membre Naturel
- Messages: 49
- Enregistré le: 30 Oct 2006, 19:50
-
 par Kiwiks » 01 Nov 2006, 18:49
par Kiwiks » 01 Nov 2006, 18:49
matteo182 a écrit:Salut,
Remarque que :
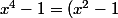(x^2 + 1))
et utilises a.
Donc en fait (x²-1)(x²+1) >= 2.2(x-1)
Je pense qu'il faut prouver que (x²+1) >= 2
alors je fait x²+1-2 >= 0
x²-1>=0
Mais là ce n'est pas toujours vrai que x²-1 >=0 :hum:
Merci ... :happy2:
-
Kiwiks
- Membre Naturel
- Messages: 49
- Enregistré le: 30 Oct 2006, 19:50
-
 par Kiwiks » 01 Nov 2006, 19:22
par Kiwiks » 01 Nov 2006, 19:22
S'il vous plait, je n'arrive pas à comprendre... Est ce que le a) est bon ?
-
leokent
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Oct 2006, 19:48
-
 par leokent » 01 Nov 2006, 20:09
par leokent » 01 Nov 2006, 20:09
Kiwiks a écrit:Donc en fait (x²-1)(x²+1) >= 2.2(x-1)
Je pense qu'il faut prouver que (x²+1)>=2
Ton raisonnement est uniquement bon si et seulement si (x^2-1)=2(x-1). Or on ne parle pas d'équation dans la question a).
Par contre, le a) est bon.
-
leokent
- Membre Naturel
- Messages: 75
- Enregistré le: 30 Oct 2006, 19:48
-
 par leokent » 01 Nov 2006, 20:20
par leokent » 01 Nov 2006, 20:20
b)(x²-1)(x²+1) >= 2.2(x-1)
(x-1)(x+1)(x^2+1) >= 4(x-1)
Soit [(x+1)(x^2+1)-4](x-1)>=0
(x^3+x+x^2+1-4)(x-1)>=0
Pour x<1, on a un produit de deux facteurs négatif ==>résultat positif
Pour x=1, le résultat est 0.
Pour x>1, on a un produit de facteurs positifis ==> résultat positif
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
