Identités remarquables au cube ?

[skater41]

Bonjour, je me souviens qu'en 2nde, le prof de maths nous avait parlé d'identités remarquables au cube, du style par contre je sais pas du tout ce que donne la forme développé et je me demande aussi si il est possible que je dois l'utiliser sur cette factorisation:

[Timothé Lefebvre]

Salut !

Oui il y a cette identité remarquable, ainsi même que etc ... Tu la trouveras sur Wiki sans doute.

[Nightmare]

Salut,

n'as-tu pas une idée qui te permettrait de trouver tout seul le développement de (a+b)^3 ? Il suffit de savoir ce que signifie "mettre au cube".

[skater41]

Et bien, si je n'avais pas trouvé sur wikipedia le développement, je ne saurais toujours pas c'est quoi :lol:

[Ericovitchi]

avec un peu d'audace

[skater41]

Le prof nous avait donné le truc pour toutes les avoir, mais je ne m'en souviens plus ... =/

En tout cas pour celle là c'est

Vous pensez que je dois utiliser ça pour l'expression à factoriser que j'ai donné dans mon premier post ?

[Ericovitchi]

non pour factoriser ça ne va pas te servir du tout car on ne voit pas d'identité remarquable évidente.

non pour factoriser ça, il faut avoir du pif et remarquer que x=i est solution ainsi que x=-i et donc que l'on peut mettre en facteur

[skater41]

Excuse moi mais, i correspond à quoi ?

[Ericovitchi]

i c'est le nombre imaginaire qui est racine de -1 donc tel que

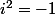
C'est sûr que si tu n'as pas encore appris les nombres complexes, tu as du mal à deviner que peut être mis en facteur.

Mais maintenant que tu le sais, alors :
?

[skater41]

?

ça me parait logique vu que c'est les seuls nombres que l'on a dans l'expression

[Ericovitchi]

Au signe près

[skater41]

Ok je pense que c'est bon merci beaucoup :)

[Ericovitchi]