salut
Remarque 3 : Ceci constitue une méthode générale de résolution des équations du second degré et des équations bicarrées.
oui et non ::
principe générale pour résoudre une équation ou une inéquation ::
1/ tout mettre dans un membre et simplifier
2/ factoriser (
le point le plus dur : voir plus bas)
3/ retourner au collège !!!
ou encore ::
appliquer la règle du produit nul pour les équations
appliquer la règle des signes pour une inéquation (avec éventuellement un tableau de signe qui est un moyen simple de représenter la résolution et l'application de cette règle)
maintenant il y a évidemment quelques exceptions :
le premier degré
le second degré (ou samouphar donne une méthode générale : le discriminant mais une autre méthode générale est
la forme canonique ... quand on connaît ses identités remarquables)
le troisième et le quatrième degré ... qui possède aussi des recettes
les (in)équations du type f(x) = f(y) ou (fx) < f(y) où f est bijective (exemple classique en terminale epx(2x + 3) < exp (4x - 5) ou ln (x^2 + x + 1) = -5 ....)
autres cas particuliers :
le changement de variable pour les équations du type bicarrées (recette la plus utilisée au lycée en générale)
derniers cas particuliers :
les cas triviaux : EX : x² + 1 = 0 ou x^4 - 1 = 0
dans le cas présent : (en ayant toujours en tête de factoriser et la forme canonique, connaissant bien les identités remarquables)
pisygma a donné une astuce pour factoriser ::
 - (a^2 + 1) = (2a^2 -1)(a^2 + 1))
donc
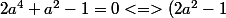(a^2 + 1) = 0 <=> 2a^2 - 1 = 0 <=> 4a^2 - 2 = 0 <=> (2a - \sqrt 2)(2a + \sqrt 2 ) = 0)
et on retourne au collège (règle du produit nul)
PS : pourquoi mets-je x² + 1 à la poubelle ?
ou encore :
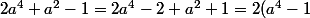 + a^2 + 1 = 2(a^2 - 1)(a^2 + 1) + a^2 + 1 = (a^2 + 1)(2a^2 - 1))
avec la même idée de pisygma ....
factorisation par la forme canonique :
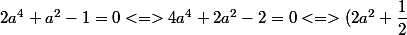^2 - \dfrac 9 4 = 0 <=> (2a^2 + 2)(2a^2 - 1) = 0 <=> ....)
en reconnaissant

REM : je multiplie par 2 pour avoir un carré parfait "simple" (avec des entiers)
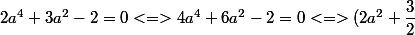^2 - \dfrac {17}4 = 0 <=> ...)
à nouveau on reconnaît x² - y² ....
^2 - \left( \sqrt 2 \right)^2 = (a^2 + 1 + \sqrt 2)(a^2 - (\sqrt 2 - 1)) = \\ \\ (a^2 + 1 + \sqrt 2)(a + \sqrt {\sqrt 2 - 1})(a - \sqrt {\sqrt 2 - 1}))

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
 grazie
grazie


