Gradient
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 18 Sep 2008, 20:04
par farator » 18 Sep 2008, 20:04
Salut,
J'ai une question un peu bête mais j'ai du mal à me représenter la situation en images dans ma tête.
Si on effectue un petit déplacement :
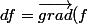.d\vec{u})
J'essaie de m'imaginer le déplacement dans le plan 3D et une courbe f.
En fait, ce déplacement est un vecteur, donc il ne suit pas la courbe, mais ses points de départ et d'arrivée appartiennent à f ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 18 Sep 2008, 20:12
par L.A. » 18 Sep 2008, 20:12
Bonsoir.
Supposons que f est une fonction C1 de R² dans R, alors on peut la représenter par une surface dans R^3. z = f(x,y)
gradf = (drondf/drondx,drondf/drondy) est un vecteur du plan R²
si du de coordonnées (dx,dy) est un "déplacement infinitésimal" dans R² (le plan des coordonnées (x,y)) à partir du point (x,y),
df = gradf(x,y).du
représente la variation correspondante de la hauteur dz en suivant la surface.
cette variation est maximale lorsque du//gradf (plus grande pente)
est nulle lorsque du et gradf sont orthogonaux (courbe de niveau)
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 18 Sep 2008, 20:37
par farator » 18 Sep 2008, 20:37
Merci beaucoup, je crois avoir compris ...
En fait si on considère du comme un vecteur c'est parce que le déplacement est infinitésimal ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 18 Sep 2008, 20:49
par L.A. » 18 Sep 2008, 20:49
Ben, du est bien un vecteur, qui représente la translation que l'on considère dans le plan (x,y), le "d" signalant qu'il est infinitésimal.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 18 Sep 2008, 21:00
par farator » 18 Sep 2008, 21:00
Euh ui bien sûr.
Et on a aussi
}{(\delta{x})}dx+\frac{(\delta{f})}{(\delta{y})}dy)
A quoi correspondent delta(f)/delta(x) et delta(f)/delta(y) ?
A la pente ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 18 Sep 2008, 21:08
par L.A. » 18 Sep 2008, 21:08
la relation dz = df/dx dx + df/dy dy
(j'ai laissé tombé les drond, mais ils sont tjs là)
traduit le fait que, lors d'un déplacement "très petit", z varie linéairement par rapport à x et y : dz = a dx + b dy
ça c'est pour les physiciens.
en maths, l'équation :
z = df/dx(x0,y0) (x-x0) + df/dy(x0,y0) (y-y0) + f(x0,y0)
est l'équation du plan tangent à la surface au point (x0,y0,f(x0,y0))
ce qui représente la meilleure approximation affine de la surface au voisinage du point (x0,y0)
donc oui, df/dx est la pente du plan tangent mesurée paralèlement à l'axe des x, et df/dy ...y.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 18 Sep 2008, 21:18
par farator » 18 Sep 2008, 21:18
Ok
dz = df/dx dx + df/dy dy
df/dx est la dérivée partielle de f par rapport à x. Si cette dérivée n'est pas une constante, et dépend de x et y, on doit remplacer x et y par x0 et y0 pour faire le calcul de dz (x0 et y0 étant les coordonnées du point de départ du déplacement infinitésimal) ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 18 Sep 2008, 21:21
par L.A. » 18 Sep 2008, 21:21
Oui.
df/dx est une fonction de R² dans R tout comme f
c'est la fonction qui à un couple (x0,y0) associe la dérivée de la fonction
g_y0 : R -> R qui à x |-> f(x,y0)
en x0.
-
farator
- Membre Irrationnel
- Messages: 1319
- Enregistré le: 16 Déc 2006, 14:03
-
 par farator » 18 Sep 2008, 21:28
par farator » 18 Sep 2008, 21:28
Merci beaucoup beaucoup L.A. !
Bonne soirée !
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 19 Sep 2008, 08:32
par L.A. » 19 Sep 2008, 08:32
Je reviens juste sur mon précédent message.
J'ai fait une erreur dans l'equation de plan que je corrige
x et y remplacés par (x-x0) et (y-y0)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
