Fondement du calcul d'intégrales
27 messages
- Page 1 sur 2 - 1, 2
Fondement du calcul d'intégrales
Bonjour à tous,
Je viens d'apprendre à faire les intégrales et comment ça marche mais je bloque sur un de ses fondements, je m'explique :
- une intégrale sert à calculer l'aire contenue sous une courbe (entre a et b par ex)
- pour calculer cette aire, on définit des rectangles de largeur infiniment petite qui vont remplir l'aire sous la courbe. La somme de ces rectangles donne l'aire sous la courbe.
- le calcul de cette aire se fait en soustrayant la primitive de a à celle de b
Mais comment la différence entre les primitives des extrémités peut refléter l'aire totale contenue sous la courbe, c'est-à-dire la somme des rectangles ? Comment cette différence peut prendre en compte les énormes variations qu'il peut y avoir entre les points a et b ?
Quelqu'un peut m'aider à comprendre ?
Merci d'avance
Je viens d'apprendre à faire les intégrales et comment ça marche mais je bloque sur un de ses fondements, je m'explique :
- une intégrale sert à calculer l'aire contenue sous une courbe (entre a et b par ex)
- pour calculer cette aire, on définit des rectangles de largeur infiniment petite qui vont remplir l'aire sous la courbe. La somme de ces rectangles donne l'aire sous la courbe.
- le calcul de cette aire se fait en soustrayant la primitive de a à celle de b
Mais comment la différence entre les primitives des extrémités peut refléter l'aire totale contenue sous la courbe, c'est-à-dire la somme des rectangles ? Comment cette différence peut prendre en compte les énormes variations qu'il peut y avoir entre les points a et b ?
Quelqu'un peut m'aider à comprendre ?
Merci d'avance
Bonsjour deneb,
Intégrer une fonction, c'est sommer (d'où la notation en S allongé si caractéristique) les variations infinitésimales d'une fonction sur un intervalle donné (les bornes de l'intervalle), d'où :
 dx)
Ce qui signifie que l'on applique f(x) à chaque minuscule variation Delta x (ou bien dx) que l'on peut comparer à des rectangles dont on fait tendre la largeur vers 0.
Intégrer une fonction, c'est sommer (d'où la notation en S allongé si caractéristique) les variations infinitésimales d'une fonction sur un intervalle donné (les bornes de l'intervalle), d'où :
Ce qui signifie que l'on applique f(x) à chaque minuscule variation Delta x (ou bien dx) que l'on peut comparer à des rectangles dont on fait tendre la largeur vers 0.
Bonsjour deneb,
Intégrer une fonction, c'est sommer (d'où la notation en S allongé si caractéristique) les variations infinitésimales d'une fonction sur un intervalle donné (les bornes de l'intervalle), d'où :
 dx)
Ce qui signifie que l'on applique f(x) à chaque minuscule variation Delta x (ou bien dx) que l'on peut comparer à des rectangles dont on fait tendre la largeur vers 0.
Edit : Mais comme le dit XENSECP, il faut aussi le voir avec la notion de primitives. Je n'en sais pas plus que vous.
Je viens de me rendre compte que j'étais parti sur quelque chose d'autre !
Intégrer une fonction, c'est sommer (d'où la notation en S allongé si caractéristique) les variations infinitésimales d'une fonction sur un intervalle donné (les bornes de l'intervalle), d'où :
Ce qui signifie que l'on applique f(x) à chaque minuscule variation Delta x (ou bien dx) que l'on peut comparer à des rectangles dont on fait tendre la largeur vers 0.
Edit : Mais comme le dit XENSECP, il faut aussi le voir avec la notion de primitives. Je n'en sais pas plus que vous.
Je viens de me rendre compte que j'étais parti sur quelque chose d'autre !
XENSECP a écrit:J'aime pas les gens qui se posent des questions métaphysiques (surtout quand tu viens d'avoir tes premiers cours sur les intégrales seulement) : tu verras ça en maths sup voilà
Merci, c'est trés contructif... Perso, j'ai besoin de comprendre pour apprendre et utiliser des outils...
XENSECP a écrit:Parce que tu n'inclus pas le "fondement de la primitive" dans ton raisonnement..
Et tu ne veux pas m'en dire plus ?
Salut,
Appelons F(x) l'aire sous la courbe de f entre a et x.
-F(x)) , c'est l'aire en rayé sur mon dessin.
, c'est l'aire en rayé sur mon dessin.
On comprend bien que, si f est continue, lorsque h va être très petit, cette aire rayée va quasiment être celle d'un rectangle de base h et de hauteur f(x). (en bleu)
Autrement dit, pour des h très petit,-F(x)\simeq hf(x)) .
.
Cela laisse présager que-F(x)}{h}=f(x)) , donc que f est la dérivée de F, ou bien que F est une primitive de f.
, donc que f est la dérivée de F, ou bien que F est une primitive de f.

Appelons F(x) l'aire sous la courbe de f entre a et x.
On comprend bien que, si f est continue, lorsque h va être très petit, cette aire rayée va quasiment être celle d'un rectangle de base h et de hauteur f(x). (en bleu)
Autrement dit, pour des h très petit,
Cela laisse présager que

Ouais et puis les sommes de Riemann pour encadrer en trapèze ou autre...
On te demande pas tellement de comprendre... mais surtout de savoir appliquer ! Le mécanisme mathématique derrière tu n'as pas besoin de le savoir ! Si tu sais que c'est F(b)-F(a) ce sera déjà bien ^^
Bah non c'est pas au programme ^^
Merci, c'est trés contructif... Perso, j'ai besoin de comprendre pour apprendre et utiliser des outils...
On te demande pas tellement de comprendre... mais surtout de savoir appliquer ! Le mécanisme mathématique derrière tu n'as pas besoin de le savoir ! Si tu sais que c'est F(b)-F(a) ce sera déjà bien ^^
Et tu ne veux pas m'en dire plus ?
Bah non c'est pas au programme ^^
XENSECP a écrit:On te demande pas tellement de comprendre...
Ben voyons. Tu ne veux pas que les élèves comprennent, et après tu t'étonnes qu'ils aient des lacunes? T'en tiens une belle toi...
Bah non c'est pas au programme ^^
Si, sa question et sa réponse sont au programme. Amusant de te voir autant parler de programmes alors que tu ne les connais pas.
Merci Nightmare pour cette réponse très claire.
Ce que je pense comprendre est que F(x) est équivqlent à f(x) pour h petit. Même raisonnement autour de a. Cependant, s'il y a une énorme variation entre a et x, cela n'est pas pris en compte ? (J'imagine que si mais je ne comprends pas pourquoi :mur: ) Parce que dans une une intrégrale, on ne calcule que la différence des primitives des bornes de l'intrégrale, non ?
Nightmare a écrit: Cela laisse présager que, donc que f est la dérivée de F, ou bien que F est une primitive de f.
Ce que je pense comprendre est que F(x) est équivqlent à f(x) pour h petit. Même raisonnement autour de a. Cependant, s'il y a une énorme variation entre a et x, cela n'est pas pris en compte ? (J'imagine que si mais je ne comprends pas pourquoi :mur: ) Parce que dans une une intrégrale, on ne calcule que la différence des primitives des bornes de l'intrégrale, non ?
J'ai un peu du mal à te suivre.
Ceci n'a pas vraiment de sens, ni F(x) ni f(x) ne dépendent de h a priori, donc dire qu'ils sont équivalent lorsque h est petit, c'est plutôt étrange.
Si j'ai bien compris pour l'histoire des variations, tu te demandes comment ça se fait qu'on effectue un calcul uniquement à l'aide des extrémités sans se soucier de ce qu'il se passe au milieu?
Si c'est bien ça, il faut te dire que dans le calcul de F(b) et celui de F(a), ce qui se passe au milieu est pris en compte.
F(b), c'est l'aire sous la courbe entre un certain point c et b.
F(a), c'est l'aire sous la courbe entre une certain point c et a.
Si c < a < b (les autres cas se traitent de la même manière) l'aire entre a et b, c'est l'aire entre c et b moins l'aire entre c et a, autrement dit, c'est F(b)-F(a).
On voit bien que ce qu'il se passe entre a et b est bien pris en compte dans le calcul de F(b) et de F(a).

Ce que je pense comprendre est que F(x) est équivqlent à f(x) pour h petit
Ceci n'a pas vraiment de sens, ni F(x) ni f(x) ne dépendent de h a priori, donc dire qu'ils sont équivalent lorsque h est petit, c'est plutôt étrange.
Si j'ai bien compris pour l'histoire des variations, tu te demandes comment ça se fait qu'on effectue un calcul uniquement à l'aide des extrémités sans se soucier de ce qu'il se passe au milieu?
Si c'est bien ça, il faut te dire que dans le calcul de F(b) et celui de F(a), ce qui se passe au milieu est pris en compte.
F(b), c'est l'aire sous la courbe entre un certain point c et b.
F(a), c'est l'aire sous la courbe entre une certain point c et a.
Si c < a < b (les autres cas se traitent de la même manière) l'aire entre a et b, c'est l'aire entre c et b moins l'aire entre c et a, autrement dit, c'est F(b)-F(a).
On voit bien que ce qu'il se passe entre a et b est bien pris en compte dans le calcul de F(b) et de F(a).

Merci de tes explications Nightmare, surtout avec les schèmas c'est parfait !
Exactement, et ton explication m'a permis de comprendre, ça fait plaisir ! Car en fait F(x) est l'aire en dessous de la courbe f(x) entre -inf et x ! Du coup, les variations entre a et b sont prises en compte.
Cependant, je réalise que ma lacune est au niveau des primitives. Ton explication dans ton post précédent est très claire et je l'ai comprise. En fait, j'essaye de faire le lien dans ma tête entre :
f(x), la valeur de la courbe en x
f'(x) (dérivée de f(x)), la pente de la courbe en x
F(x), (primitive de f(x)), l'aire dessous de la courbe f(x)
Ce que j'ai du mal à saisir, c'est comment l'opération inverse de la dérivée (qui donne donc la pente d'une courbe, nombre correspondant à un fait localisé) peut donner une aire (nombre correspondant à une surface entre -inf et x)...
Je me prends peut-être trop la tête...
Nightmare a écrit:Si j'ai bien compris pour l'histoire des variations, tu te demandes comment ça se fait qu'on effectue un calcul uniquement à l'aide des extrémités sans se soucier de ce qu'il se passe au milieu?
Exactement, et ton explication m'a permis de comprendre, ça fait plaisir ! Car en fait F(x) est l'aire en dessous de la courbe f(x) entre -inf et x ! Du coup, les variations entre a et b sont prises en compte.
Cependant, je réalise que ma lacune est au niveau des primitives. Ton explication dans ton post précédent est très claire et je l'ai comprise. En fait, j'essaye de faire le lien dans ma tête entre :
f(x), la valeur de la courbe en x
f'(x) (dérivée de f(x)), la pente de la courbe en x
F(x), (primitive de f(x)), l'aire dessous de la courbe f(x)
Ce que j'ai du mal à saisir, c'est comment l'opération inverse de la dérivée (qui donne donc la pente d'une courbe, nombre correspondant à un fait localisé) peut donner une aire (nombre correspondant à une surface entre -inf et x)...
Je me prends peut-être trop la tête...
Si tu vois la dérivée comme une pente, ça ferme assez la vision de la chose, puisque ça se cantonne à un dessin.
Il faut voir la dérivée comme un accroissement, linéaire.
Imaginons par exemple que f'(5)=2. Cela se traduit par le fait que si je cherche à calculer l'image d'un point proche de 5, un certain 5+h avec h petit, alors mon accroissement par rapport à f(5) est quasiment égal à 2h. Autrement dit, f(5+h)=f(5)+2h
Si f'(10)=-40, alors pour des h très petit,\simeq f(10)-40h)
etc.
Plus généralement, pour n'importe quel point x,\simeq f(x)+f'(x).h)
C'est ce point de vue "approximation affine" qu'il faut adopter au plus vite pour comprendre la notion de dérivée.
Si tu as compris ça, relis ma première explication qui devrait répondre à ta question sur la dualité entre dérivée / primitive
Il faut voir la dérivée comme un accroissement, linéaire.
Imaginons par exemple que f'(5)=2. Cela se traduit par le fait que si je cherche à calculer l'image d'un point proche de 5, un certain 5+h avec h petit, alors mon accroissement par rapport à f(5) est quasiment égal à 2h. Autrement dit, f(5+h)=f(5)+2h
Si f'(10)=-40, alors pour des h très petit,
etc.
Plus généralement, pour n'importe quel point x,
C'est ce point de vue "approximation affine" qu'il faut adopter au plus vite pour comprendre la notion de dérivée.
Si tu as compris ça, relis ma première explication qui devrait répondre à ta question sur la dualité entre dérivée / primitive
Autre explications
Si la fonction est continue sur [a,b] elle est intégrable sur [a,b]
est continue sur [a,b] elle est intégrable sur [a,b]
alors pour tout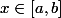
=\int_{ a }^{ x } f(t) dt) est LA primitive de la fonction
est LA primitive de la fonction  qui s'annule en
qui s'annule en  c'est à dire qui vérifie
c'est à dire qui vérifie =0) (voir le PS à la fin de ce message)
(voir le PS à la fin de ce message)
On peut donc écrire
=\int_{ a }^{ b } f(t) dt =F(b)-F(a)) (car
(car =0) )
)
ou par la relation de Chasles sur l'intégrale
 dt =\int_{ a }^{ x } f(t) dt +\int_{ x }^{ b } f(t) dt =\int_{ a }^{ x } f(t) dt - \int_{ b }^{ x } f(t) dt =[F(x)-F(a)]-[F(x)-F(b)]=F(b)-F(a))
De plus comme toutes les primitives de la fonction
de la fonction  s'écrivent G(X)=F(x)+ constante
s'écrivent G(X)=F(x)+ constante
on a également
 dt =G(b)-G(a))
PS)
le fait que la fonction soit continue sur [a,b] , fais que la fonction
soit continue sur [a,b] , fais que la fonction  est dérivable sur [a,b]
est dérivable sur [a,b]
et on a :=f(x)) donc la fonction
donc la fonction  est bien une primitive de la fonction
est bien une primitive de la fonction 
De plus comme dt =0) on a bien
on a bien =0)
On peut donc écrire que : dt =F(x)-F(a))
Si la fonction
alors pour tout
On peut donc écrire
ou par la relation de Chasles sur l'intégrale
De plus comme toutes les primitives
on a également
PS)
le fait que la fonction
et on a :
De plus comme
On peut donc écrire que :
Bonjour NightmareNightmare a écrit:A quel moment justifies-tu que F'(x)=f(x)?
Je ne le démontre pas , je l'admets
sinon il faut montrer que F est une fonction dérivable et par un calcul de la limite du taux de variation de la fonction F entre x et x+h quand h tend vers 0 que ce nombre dérivée est f(x)
Remarque :
Je ne sais pas si c'est vraiment une préoccupation pour l'auteur de ce topic (qui est au lycée et donc qui admet certains théorèmes...)
Salut NightmareNightmare a écrit:C'est principalement sa préoccupation dans ce topic ....
Si tu le dis c'est que tu dois avoir raison, mais ce n'est pas ce que je pense....
Juste pour information : je te rappelle le début du message de deneb dans son 1ier message de ce topic :
"Je viens d'apprendre à faire les intégrales et comment ça marche et...."
Je ne vois aucun intérêt de démontrer ce "théorème" , mais comme tu le demandes , je le fais....
Merci d'expliquer pourquoi tu insistes sur cette question.
La question est donc de démontrer qu'une fonction continue
On va donc démonter que la fonction
Soit
Calcul de
donc
Or
donc
cqfd
Commentaire :
La "continuité" d'une fonction est une condition suffisante mais pas nécessaire : toute fonction continue est "une dérivée" mais cela ne veut pas dire que seules les fonctions continues ont des primitives....
Merci à l'auteur de ce topic (à deneb) de réagir, s'il veut, pour poser d'autres questions/commentaires sur son topic
Ce topic est un sujet très intéressant car il rapproche 2 concepts complétement différents
1) la notion d'intégrale et d'aire
2) la notion de primitive et de dérivation
EDIT(MAJ)
Ce message a été corrigé (necessaire devient suffisant....)
Ce message va s'autodétruire dans 24H
schulhof_2 a écrit:Salut Nightmare
Si tu le dis c'est que tu dois avoir raison, mais ce n'est pas ce que je pense....
Juste pour information : je te rappelle le début du message de deneb dans son 1ier message de ce topic :
"Je viens d'apprendre à faire les intégrales et comment ça marche et...."
Je ne vois aucun intérêt de démontrer ce "théorème" , mais comme tu le demandes , je le fais....
Merci d'expliquer pourquoi tu insistes sur cette question.
As-tu lu le topic en entier?
Quand je lis le premier post de l'auteur, la question qui apparaît clairement est celle que tu éludes en partie.
Je la cite :
Mais comment la différence entre les primitives des extrémités peut refléter l'aire totale contenue sous la courbe, c'est-à-dire la somme des rectangles ? Comment cette différence peut prendre en compte les énormes variations qu'il peut y avoir entre les points a et b ?
Es-tu sûr que ton post réponde bien à ces questions?
En outre, l'auteur m'a clairement signalé que ma réponse, bien qu'il ne la comprenait que partiellement, répondait bien à ses questions.
Attention, il n'est en aucun cas question de comparer la qualité de nos réponses, je te signale juste qu'a priori, tu ne réponds pas entièrement aux questions que se pose l'auteur. Cela ne veut pas dire que ta réponse est inutile.
Concernant ta démonstration que F'(x)=f(x), qu'est-ce qui justifie l'existence de
Sinon, tu dis :
Commentaire :
La "continuité" d'une fonction est une condition nécessaire mais pas suffisante
C'est l'inverse, la continuité est suffisante mais pas nécessaire (il n'est pas nécessaire d'être une fonction continue pour avoir des primitives)
Je suis par contre d'accord avec :
: toute fonction continue est "une dérivée" mais cela ne veut pas dire que seules les fonctions continues ont des primitives....
@Nightmare
Je ne comprend pas l'objet de ton message....
Tu m'as demandé de démontrer un théorème , je l'ai fait, tu n'es toujours pas satisfait..
C'est ton problème, par le mien...
Je sais très bien que tu as compris cette démo et s'il faut l'expliquer dans les détails , merci de le faire, car en ce qui me concerne je n'ai fait que répondre à un tes messages (et non pas à un message de l'auteur du topic).
Je participe à ce topic uniquement pour donner des infos supplémentaires à ce topic sur des notions de continuité, primitives et dérivée..
Ni plus Ni moins....
Je n'ai pas envie de polémiquer avec toi ET donc , c'est bon , je suis même prêt à effacer mes différents messages pour ne pas poluer "ce topic" plus longtemps avec des "inepties"
Je le fais dès demain soir le temps que l'auteur du topic puisse au moins une fois lire le seul message que j'ai écrit pour lui.
Mes autres messages ne sont que pour répondre à des questions que tu connais très bien...
Quel est l'intérêt ?
RAZ
Comme cela dans ce topic , on reviendra 24H avant...
comme si j'avais rien écrit dans ce topic.... et comme cela tu pourras faire et écrire ce que tu veux à l'auteur....
ps)
je corrige le lapsus nécessaire/suffisant dans mon message
Merci pour ton aide.
Je ne comprend pas l'objet de ton message....
Tu m'as demandé de démontrer un théorème , je l'ai fait, tu n'es toujours pas satisfait..
C'est ton problème, par le mien...
Je sais très bien que tu as compris cette démo et s'il faut l'expliquer dans les détails , merci de le faire, car en ce qui me concerne je n'ai fait que répondre à un tes messages (et non pas à un message de l'auteur du topic).
Je participe à ce topic uniquement pour donner des infos supplémentaires à ce topic sur des notions de continuité, primitives et dérivée..
Ni plus Ni moins....
Je n'ai pas envie de polémiquer avec toi ET donc , c'est bon , je suis même prêt à effacer mes différents messages pour ne pas poluer "ce topic" plus longtemps avec des "inepties"
Je le fais dès demain soir le temps que l'auteur du topic puisse au moins une fois lire le seul message que j'ai écrit pour lui.
Mes autres messages ne sont que pour répondre à des questions que tu connais très bien...
Quel est l'intérêt ?
RAZ
Comme cela dans ce topic , on reviendra 24H avant...
comme si j'avais rien écrit dans ce topic.... et comme cela tu pourras faire et écrire ce que tu veux à l'auteur....
ps)
je corrige le lapsus nécessaire/suffisant dans mon message
Merci pour ton aide.
27 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
