DM fonctions trinomes (1ère)

[Anonyme]

salut, j'ai un DM sur les fonctions que je trouve super dur. Aidez moi svp, voici le sujet:(j'ai réussit à faire le 1° mais c'est tout)
dans un repère (O,i,j), on note C le cercle d'équation x^2+y^2-6x+4y-12=0
et Dm la droite d'équation 4x-3y+m =0. Ainsi à chaque réel m correspond une droite Dm.
1° Trouver les réel a ,b et r tel que x^2+y^2-6x+4y-12=(x-a)^2+(y-b)^2-r^2.En déduire les coordonnées du centre de C et son rayon .(tracer C)
2°Discuter selon les valeurs de m le nombre de points d'intersection de Dm avec C. interpréter graphiquement les résultats.
3°Trouver les coordonnées des points d'intersection T1 et T2 dans les deux cas où Dm est tangente à C ?
4°Dans le cas où Dm coupe C en deux points qu'on appelle Am et Bm, trouver les coordonnées de Im milieu de [AmBm].Où se situe Im par rapport au segment [T1T2]?
RAPPELS: vecteur AB(xB-xA, yB-yA)
AB^2=(xb-xa)^2+(yb-ya)^2
le milieu du segment [AB] a pour coordonnées (xa+xb/2;ya+yb/2)
merci d'avance

[becirj]

Bonjour
2. Dans l'équation de la droite, on calcule y en fonction de x et on remplace dans l'équation du cercle. On obtient ainsi une équation du second degré d'inconnue x avec des coefficients qui dépendent de m.
On calcule le discriminant qui dépend de m.
Il y a 2 points d'intersection pour les valeurs de m telle que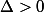 ; il y a un point de tangence si 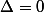et la droite est extérieure au cercle si

[Popo]

3°)Pour trouver les points d'intersections , il te suffit de résoudre
4x-3y+m = x^2+y^2-6x+4y-12 (je n'ai pas calculé la première question mais je pense que si tu calcules 4x-3y+m = (x-a)^2+(y-b)^2-r^2 avec les valeurs a,b,r que tu as trouvé ce sera plus simple )

[becirj]

La méthode de Popo conduit à une équation du second degré à 2 inconnues qu'on ne sait pas résoudre.

[Popo]

et l'identification ?

[André]

Bonjour !
Ce problème devient simple si on y va TRES progressivement.
1) Pour vérifier, je trouves a=3, b=-2 et r=5
J'espère que je n'ai pas fait d'erreur au moins ^^
2) Becirj a raison
Dm : y = 4x/3+m/3
En remplaçant y dans l'équation du cercle on trouve :
(1) 25x² + (8m-6)x + (m²+12m-108) = 0
rem : j'ai multiplié par 9 pour simplifier l'équation
Résoudre (1), c'est trouver l'abscisse x du point d'intersection entre Dm et C.
Deux constatations : l'équation donc la solution x dépend de m ; il peut y avoir 0, 1 ou 2 solutions.
Effectivement, 0 solution signifie que Dm ne coupe pas C, 1 que Dm passe par 1 point de C (Dm tangente à C) et 2 que Dm passe par 2 points de C ; ces points étant d'abscisse x.
Pour cela on calcule le discriminant Delta1(m) de (1) qui dépend de m :
je trouve Delta1(m) = -36(m²+36m-301)
Le signe de Delta1(m) donne le nombre de solutions de (1).
Regardons d'abord le signe de m²+36m-301. Cette fonction de m est une parabole en "U" (coefficient d'ordre 2 > 0) : elle décroît puis croît. Elle coupe également l'axe des abscisses (coefficients d'ordre 2 et 0 de signes opposés) : Elle est donc positive, décroît pour devenir négative à partir de m = x1, puis croît pour devenir positive à partir de m = x2. m²+36m-301 est donc positif pour m < x1 et m > x2, négatif pour x1 < m < x2.
Il suffit de calculer x1 et x2 les solutions de m²+36m-301 = 0 :
je trouve x1 = -43 et x2 = 7 (pas d'erreur ?)
Avec -36 en facteur Delta1(m) est donc négatif pour m < -43 et m > 7, positif pour -43 < m < 7. On en déduit alors le nombre de points d'intersection en fonction de m.
3) Il suffit de résoudre (1) avec m = -43 d'une part et m = 7 d'autre part. Delta1(m) = 0 dans ces deux cas (normal !). Pour m = 43, je trouve x43 = 7 ; pour m = 7, je trouve x7 = -1. Avec l'équation de Dm, on retrouve les ordonnées respectives de ces points : y43 = -5 ; y7 = 1.
Voilà ! En espérant ne pas avoir fait d'erreur !

[André]

J'oubliais le 4)
Avec T1(7 ; -5) et T2(-1 ; 1), le vecteur T1T2 vaut (-8 ; 6)
Il faut d'abord trouver les abscisses xAm et xBm de Am et Bm, au moins dans leurs expressions générales. Elles sont solutions de (1) :
xAm = [-(8m-6) - sqrt(Delta1(m))]/(2*25) (sqrt : racine)
xBm = [-(8m-6) + sqrt(Delta1(m))]/(2*25)
Sans développer, l'abscisse de Im, qui vaut (xAm+xBm)/2, est xIm = (3-4m)/25 (pas de delta1(m) !)
Comme le segment [AmBm] est dans la droite Dm, Im est sur Dm, d'où son ordonnée obtenue avec l'équation de Dm :
yIm = (12+9m)/75
On calcule le vecteur T2Im : ((84-12m)/75 ; (-63+9m)/75)
On se doute bien que Im est sur [T1T2] ; il suffit de le vérifier en montrant que T1T2 et T2Im sont colinéaires : en effet, x(T1T2)*y(T2Im) - y(T1T2)*x(T2Im) = 0.
Voilà ! L'important c'est de bien comprendre le sujet et de le traiter calmement pas à pas. Bonne chance !