Fonctions et coordonnées...

[Hardtoexplain91]

Bonjour, jai un exercice à faire, il est long certes, mais j'aimerais vraiment avoir de l'aide. J'en nécessite même... je commence vraiment à avoir des lacunes en maths en première et j'ai vraiment pas envie de couler, surtout qu'on est au deuxième trimestre.
Je ne demande pas de faire mon exercice, mais de m'expliquer et de m'aider à le résoudre. Svp.

Merci et j'espère qu'on me répondra...
Bonne soirée.

Soit P et P' les courbes d'équations cartésiennes respectives y=racine(x+1/4) et y=-racine(x+1/4)
a) Préciser l'ensemble de définition de la fonction f définie par : f(x)=racine(x+1/4)
En déduire le sens de variation de la fonction f à partir du sens de variation de la fonction u : x=> racinex

b) Sans faire le garphique, expliquer comment construire les courbes P et P'.
c) Le point M, de coordonnées cartésiennes (x,y) et de coordonnées polaires (r, teta) est un point de la courbe P.
- Démontrer que r supérieur ou égal à 1/4
- Démontrer que r²=x²+x+1/4. Et en déduire que r= x+1/2
- Soit D la droite d'équation x=-1/2 et H le projeté orthogonal de M sur D. Interpréter géométriquement la relation r= x+1/2
- Faire une figure
- Démontrer que, pour teta appartenant à ] O, pi[ r = 1/2(1-costeta)
d) Démontrer que tout point P dont les coordonnées polaires vérifient r=1/2(1-costeta) avec teta appartenant à ]O,2pi[, est un point de P ou de P'.

[Monsieur23]

Qu'as-tu fais pour l'instant ?

La question a) est une application directe de ton cours ! :happy2:

[Hardtoexplain91]

Jai rien fait et cest bien ca le probleme. Jaimerais dj comprendre lexercice,
pouvez vous maider a faire cet exercice, si ca vous derange pas bien sur...
parce que jen ai vraiment marre de ramer en maths t-t

[Monsieur23]

Pour la a), tu ne peux prendre la racine d'un nombre que s'il est POSITIF.

Donc f est définie pour tous les x vérifiant

Ensuite, f est la composée de deux fonctions croissantes ( ), donc elle est croissante.

Pour la b) : La courbe de f n'est jamais que la courbe de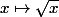 , mais un petit peu décalée vers la gauche ( je te laisse rédiger ça )
Et c'est pareil pour -f.

Pour la c) :
Hum, je serais toi, je ferais d'abord la question suivante.
Tu as .
Tu développes, tu factorises, et tu trouves le bon résultat.
Ensuite, tu cherches le minimum de r, quand x est plus grand que -1/4.

Commence par ça, je regarde le reste.

[Hardtoexplain91]

ok, merci je regarde ce que vous avez fait.

[Monsieur23]

Pour l'interprétation géométrique, je vois pas trop.

Ensuite :
Tu as
De plus, tu as démontré

Donc
Tu en tires r.

J'dois y aller, j'te laisse faire la dernière question.

[Hardtoexplain91]

Dsl, jai pas compris votre B et votre C :s

[Hardtoexplain91]

SVP; aidez moi...

[Hardtoexplain91]

Bonsoir, jai reussi a le faire juska la 4.


Quelquun pourrait il maider pour la 5?

Je bloque dessus.