Bonsoir,
Je ne vois pas quelle méthode utiliser pour résoudre l'exercice suivant :
Soit b un réel et f la fonction : f(x) = (-x²+bx+3)/(x-1)
a) Déterminer les réels b tels que f n'ait pas d'extremums.
b) Déterminer alors la valeur de b pour laquelle f admette au point d'abscisse 2 une tangente parallèle à la droite d'équation 2x+2y-3=0.
J'ai d'abord calculé l'ensemble de définition qui est : Df = IR {1}
Pour la question a, j'ai testé plusieurs valeur de b et j'ai vu que si b=-2, alors la fonction f n'a pas d'extremums.
Fonctions avec un inconnu
4 messages
- Page 1 sur 1
Bonsoir charly45,
Pour le a), tu sais que si f' s'annule et change de signe en , alors f admet un extremum local en
, alors f admet un extremum local en  .
.
Il te suffit donc de calculer la dérivée de ta fonction et de choisir b de sorte que f' ne s'annule pas ou s'annule une fois (car tu arriveras à une équation du second degré).
Pour la suite, tu dois utiliser l'équation de la tangente à la courbe au point d'abscisse a :
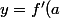(x-a) + f(a)) .
.
Sh0nty
Pour le a), tu sais que si f' s'annule et change de signe en
Il te suffit donc de calculer la dérivée de ta fonction et de choisir b de sorte que f' ne s'annule pas ou s'annule une fois (car tu arriveras à une équation du second degré).
Pour la suite, tu dois utiliser l'équation de la tangente à la courbe au point d'abscisse a :
Sh0nty
Merci pour vos réponses !
Pour le a), j'ai calculé la dérivée, puis j'ai cherché le discriminant du numérateur, puis j'ai résous l'inéquation 0. J'ai obtenu b
0. J'ai obtenu b -2
-2
Pour le b) :
y=f'(a)(x-a)+f(a)
a=2
f'(2) =^2+2*2-b-3}{(2-1)^2})
f'(2) =
f'(2) = 5-b
f(2) =^2+b*2+3}{2-1})
f(2) =
f(2) = 7+2b
y=(5-b)(x-2)+(7+2b)
y = 5x-3+4b-bx
Je suis bloqué à cette endroit.
Pour le a), j'ai calculé la dérivée, puis j'ai cherché le discriminant du numérateur, puis j'ai résous l'inéquation
Pour le b) :
y=f'(a)(x-a)+f(a)
a=2
f'(2) =
f'(2) =
f'(2) = 5-b
f(2) =
f(2) =
f(2) = 7+2b
y=(5-b)(x-2)+(7+2b)
y = 5x-3+4b-bx
Je suis bloqué à cette endroit.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
