Fonction Inverse Ou Affine

[thepilot08]

bonjour, j'ai cette fonction: x+4/x
je dois prouver quelle est croissante sur [2 ;+l'infini[
mais j'ai un doute car elle ressemble à une fonction inverse mais puisqu'elle est croissante sur [2;+li'nfini[ et donc je ne sais pas comment justifier cela et aussi est ce que le premier "x" est le coeficient directeur ?

Merci

[Mortelune]

Bonjour, elle n'est ni l'un ni l'autre, c'est juste une somme d'une fonction linéaire avec une fonction inverse.

Par contre pour montrer la croissance tu peux calculer le signe de f(x)-f(y) pour x>y non ?

(je suppose que tu es en 2nde ?)

[thepilot08]

Que veut tu dire ? par calcule le signe de f(x)-f(y) pout x>y moi en cour je travail avec a et b je sais que sa change pas grand chose mais puisque je ne sais pas quelle fonction est-ce je ne sais pas par ou commencer car dans mes cours j'ai beaucoup de démonstration mais aucune ne corespond à cette fonction

[Mortelune]

La démonstration sert plus dans l'esprit que dans la simple recopie. Pour ce que je veux dire, j'ai nommé f la fonction que tu as présenté, et j'ai appliqué la définition d'une fonction croissante : si pour tout x>y on a f(x)>f(y) alors al fonction est croissante.

Pour le montrer on s'intéresse donc au signe de f(x)-f(y).

[thepilot08]

ok mais le probleme c'est que c'est également la même chose dans l'interval [0;2]

[Mortelune]

Déjà si tu pouvais le faire pour l'intervalle demandé ça serait un plus. Pour [0;2] j'ai de sérieux doutes sur le fait que ce soit le même résultat.

[Adoration_For_None]

Ce que veux essayer de te faire comprendre Mortelune c'est ceci :

Considérons une fonction f tel que .
Nous voulons prouver que f décroit sur .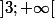
On suppose , car la fonction inverse décroit sur .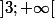
Ainsi : , car 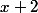est positif sur .
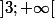On reconnait et .
On conclut donc que .
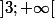Ainsi : décroit sur , car l'ordre des images est inversé.

Je t'ai donné le modèle tu n'as plus qu'à faire la même chose avec ta fonction, tu peux poster ton résultat ici, je regarderai ta démarche. Bon courage !

[thepilot08]

Merci exuse moi pour le retard je la posterai demain matin

[Adoration_For_None]

Merci exuse moi pour le retard je la posterai demain matin

Pas de problème.

[thepilot08]

F(x)= x+2/x-3
adonc a-3donc 1/a-3>1/b-3
x+2>0
donc a+2/a-3>b+2/b-3
donc f(a)>f(B)
donc la fonction est croissante sur l'interval ]2;+l'infini[

[Adoration_For_None]

F(x)= (x+2)/(x-3)
a1/(b-3), car la fonction inverse décroit sur ]3;+infini[
x+2>0 sur ]3;+infini[
donc (a+2)/(a-3)>(b+2)/(b-3)
donc f(a)>f(b) [c'est sûrement une faute de frappe, tu avais mis "B" au lieu de "b"]
donc la fonction est croissante sur l'intervalle ]3;+l'infini[

C'est juste Dans un soucis de rigueur précise certaines choses, je t'ai mis les modifications en rouges.

[Mortelune]

C'e serait pas plutôt un -2 au lieu du 2 sur cet exemple pour être aussi rigoureux dans le résultat que sur le raisonnement ?

Et puis maintenant il faut adapter ce résultat à la première fonction :)

[Adoration_For_None]

Je viens de tracer sur ma calculatrice, et c'est sur que la fonction est décroissante, ce qui est logique vu que 3 annule le dénominateur.
Je corrige ça dans mon post

[Mortelune]

En refaisant cette étude il faut commencer par faire 2 cas :

a>b>3 et b
Et pour a ou b>-2 la multiplication par a+2 ou b+2 ne change pas l'ordre alors que dans le cas contraire si.

En fait l'exemple est plus compliqué que l'exercice :we: