Fonction composée

[chelsea-asm]

Bonjour,

Nous sommes en train de voir les fonctions composées. Et nous avons vu deux formules :

g(ax+b) = a x g'(ax+b)

et

g'(x) = a x f'(ax+b)

J'en déduis donc que :
g(ax+b) = a x g'(ax+b)
donc
f(ax+b) = a x f'(ax+b) et g'(x) = a x f'(ax+b)
alors est-ce que f(ax+b) = g'(x) ?

[Ericovitchi]

Heu ça n'est pas vraiment clair tes notations.
Je suppose que tu veux dire que
[g(ax+b)]' = a x g'(ax+b) ou [f(ax+b)]' = a x f'(ax+b) oui c'est exact

Cela dit je n'ai rien compris à la relation qui lie f et g et quelle est réellement ta question ?

[chelsea-asm]

Ah non désolé, en cours on a vu :

g(ax+b) = a x g'(ax+b)

et

g'(x) = a x f'(ax+b)

c'est faux ce qu'on a vu en cours alors ? :doh:

[Ericovitchi]

C'est quoi l'énoncé ? on recherche deux fonctions particulières telle que
g(ax+b) = a x g'(ax+b) et g'(x) = a x f'(ax+b) ? C'est ça ?

C'est quoi la question ?

[chelsea-asm]

Ben non il n'y a pas d'énoncé, c'est un cours, une leçon avec les formules.
J'ai remarqué que les deux formules se ressemblaient.
g(ax+b) = a x g'(ax+b)
et
g'(x) = a x f'(ax+b)

alors je me suis dit que si pour la première f(ax+b) = a x f'(ax+b)
alors on devrait avoir g'(x) = f(ax+b) vu que c'est la même formule pour les deux.
Mais je suis pas sûr. Alors je voulais savoir si quelqu'un l'avait déjà fait et qui pourrait m'aider.
Merci

[Ericovitchi]

Alors si c'est du cours, on a simplement voulu t'expliquer que la dérivée d'une fonction g(ax+b) c'était ag'(ax+b)
donc [g(ax+b)]' = a x g'(ax+b)

C'est le cas particulier de la dérivée d'une composition de fonctions
[f(g(x)]'= f'(g(x)).g'(x)

Par exemple la dérivée de sin (ax+b) c'est a cos (ax+b)
la dérivée de (ax+b)² c'est 2a(ax+b)

Donnes moi la dérivée de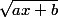 histoire de voir si tu as compris ?

[chelsea-asm]

alors
=

[chelsea-asm]

alors
=

C'est ça ?

[Ericovitchi]

non il faut qu'il reste des x quelque part

[massengo]

C'est faux inspire toi de la formule [f(g(x)]'= f'(g(x)).g'(x).
tu poses g(x)=ax+b et f(x)=racine(x) donc f(g(x))=f(ax+b)=racine(ax+b).
alors la reponse sera ?

[massengo]

f '(g(x))=1/2racine(g(x))=1/2racine(ax+b)
g '(x)=a alors [f(g(x)]'= f'(g(x)).g'(x)=a[1/2racine(ax+b)]=a/2racine(ax+b)