Famille libre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 13:05
par juju78 » 14 Mar 2009, 13:05
Bonjour
On a :
(2a + 1)x - ay - az = 0
2ay - z = 0
x - ay + (1 - a)z = 2
On me demande a quelles conditions sur a, la famille constituée des vecteurs v1; v2; v3 est elle libre ? que peut t'on déduire sur A(a)?
On sait qu'une famille est libre ssi pour tout


,


= 0 implique
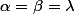
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 15:01
par uztop » 14 Mar 2009, 15:01
Bonjour,
est ce que tu as essayé de résoudre le système ?
On peut presque toujours déterminer x,y et z de façon unique par rapport à a, et on ne peut donc pas avoir de famille libre.
Reste maintenant à étudier les cas particuliers où on ne peut pas résoudre le système.
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 15:07
par juju78 » 14 Mar 2009, 15:07
Si a=0 > systeme indeterminé?
Si a=-1/2 ou a=1 > systeme impossible
Si a different de 0, -1/2, 1 : syteme de Cramer ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 16:45
par uztop » 14 Mar 2009, 16:45
quand le système est indéterminé, ça laisse des degrés de liberté et on peut donc avoir une famille libre.
Sinon, quand le système est impossible, ou quand il a une solution unique, on ne peut pas avoir de famille libre.
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 16:50
par juju78 » 14 Mar 2009, 16:50
toutefois je crois m'etre trompé pour a=0 ce serait plutot impossible non?
Je n'ai aucun moyen de verification et je ne suis pas sure pouvez vous m'aider ? :$
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 17:05
par uztop » 14 Mar 2009, 17:05
oui, pour a=0, le système devient
x=0
-z=0
x+z=2
ce qui est impossible.
Sinon, pour a=-1/2, je n'ai pas l'impression que le système est impossible (sauf erreur de calcul)
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 17:12
par juju78 » 14 Mar 2009, 17:12
ben il me semble, sur la derniere ligne de calcul j'ai
0 0 2a²-a-1 | -4a-2
donc si a=-1/2 c'est impossible ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 17:19
par uztop » 14 Mar 2009, 17:19
je comprends pas ce que tu as écrit.
Voilà ce que j'ai fait: pour a=-1/2, le système devient:
y/2+z/2=0
-y-z=0
x+y/2+3z/2=2
Ce qui donne une infinité de solutions.
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 17:25
par juju78 » 14 Mar 2009, 17:25
j'ai utilisé gauss et la resolution sous forme matricielle pourtant
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 17:27
par uztop » 14 Mar 2009, 17:27
si tu as trouvé un déterminant nul, ça ne veut pas dire que le système est impossible, il peut aussi avoir une infinité de solutions (ce qui est le cas ici)
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 17:34
par juju78 » 14 Mar 2009, 17:34
dans notre cours il y a écrit que lorsqu'il y a une ligne de 0 et que la solution est differente de 0 alors c'est impossible
par exemple on ne peut avoir 0x+0z = 3
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 17:39
par uztop » 14 Mar 2009, 17:39
oui en effet, mais sauf erreur de ma part, on ne tombe pas sur une ligne de 0
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 17:42
par juju78 » 14 Mar 2009, 17:42
a oui effectivement , merci! :)
Par ailleurs le systeme admet bien une unique solution pour a different de 0 de -1/2 et de 1 ? (on demande pas de la determiner)
et donc pour a= -1/2 le systeme est indeterminé, et comment faire pour la famille libre.?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 18:09
par uztop » 14 Mar 2009, 18:09
excuse moi, je me suis un peu embrouillé (je suis parti sur la résolution du système alors que ce n'était pas vraiment la question posée...)
Bon, ce qu'il faut faire ici, étant donné que tu as autant de vecteurs que la dimension de l'espace, c'est de calculer le déterminant du système. S'il est non nul, la famille est libre.
Un déterminant non nul, c'est équivalent à une solution unique du système, donc tu as la réponse (mais on n'a probablement pas choisi la solution la plus rapide)
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 18:14
par juju78 » 14 Mar 2009, 18:14
Mais ça va dependre de a , quelles valeurs prendre pour a ?
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 14 Mar 2009, 18:25
par uztop » 14 Mar 2009, 18:25
tu dois trouver les valeurs de a pour lesquelles la famille est libre, c'est à dire pour lesquelles le déterminant est non nul.
On a vu que celui ci est non nul pour a différent de 0, -1/2 et 1.
C'est donc la réponse à la question posée ici.
-
juju78
- Membre Rationnel
- Messages: 850
- Enregistré le: 13 Avr 2006, 16:05
-
 par juju78 » 14 Mar 2009, 18:35
par juju78 » 14 Mar 2009, 18:35
La question exacte etait : a quelles conditions sur a, la famille constituée des vecteurs v1; v2; v3 est elle libre ? que peut t'on déduire sur A(a)?
Les conditions sont que a soit different de 0 -1/2 et 1
Mais que peut t(on déduire sur A(a) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités