Factorisation indication
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
demodocos
- Messages: 5
- Enregistré le: 20 Sep 2012, 18:39
-
 par demodocos » 21 Sep 2012, 05:58
par demodocos » 21 Sep 2012, 05:58
Bonjour j'ai 35 ans je me remets un peu aux maths et j'aimerai s'il vous plaît une petite indication quant à cette factorisation que je ne comprends pas....
(x-1)^3+64=(x-1+4)[(x-1)^2-(x-1)4+16]
=(x+3)(x^2-6x+21)
Comme vous le voyez j'ai le résultat,mais le raisonnement me fait défaut,..merci
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 21 Sep 2012, 08:51
par titine » 21 Sep 2012, 08:51
Il faut savoir que :
a^3 + b^3 = (a + b)(a² - ab + b²)
Facile à vérifier en développant.
-
titine
- Habitué(e)
- Messages: 5574
- Enregistré le: 01 Mai 2006, 13:59
-
 par titine » 21 Sep 2012, 12:48
par titine » 21 Sep 2012, 12:48
Autre méthode :
(x-1)^3+64
On remarque que -3 est racine car pour x=-3 :
(x-1)^3+64 = (-4)^3 + 64 = -64 + 64 = 0
Donc on peut mettre (x - (-3)) = (x+3) en facteur :
(x-1)^3+64 = (x+3)(................)
Et on cherche par quoi multiplier (x+3) pour trouver x^3 - 64 ..............
-
demodocos
- Messages: 5
- Enregistré le: 20 Sep 2012, 18:39
-
 par demodocos » 21 Sep 2012, 18:46
par demodocos » 21 Sep 2012, 18:46
titine a écrit:Il faut savoir que :
a^3 + b^3 = (a + b)(a² - ab + b²)
Facile à vérifier en développant.
Bien sûr!!! les identités remarquables de degré 3 existent aussi,suis-je bête(vous nêtes pas obligée de répondre :lol3: )
-
demodocos
- Messages: 5
- Enregistré le: 20 Sep 2012, 18:39
-
 par demodocos » 21 Sep 2012, 18:50
par demodocos » 21 Sep 2012, 18:50
titine a écrit:Autre méthode :
(x-1)^3+64
On remarque que -3 est racine car pour x=-3 :
(x-1)^3+64 = (-4)^3 + 64 = -64 + 64 = 0
Donc on peut mettre (x - (-3)) = (x+3) en facteur :
(x-1)^3+64 = (x+3)(................)
Et on cherche par quoi multiplier (x+3) pour trouver x^3 - 64 ..............
Là je suis encore à des années lumière de votre raisonnement,chapeau bas :doh:
Merci encore pour votre aide,je vais travailler un peu quelques exos de ce genre pour me remettre dans le bain j'en ai besoin,à bientôt.
-
nodjim
- Membre Complexe
- Messages: 3241
- Enregistré le: 24 Avr 2009, 16:35
-
 par nodjim » 21 Sep 2012, 19:09
par nodjim » 21 Sep 2012, 19:09
Ou encore
(x-1)^3= -(1-x)^3
64=4^3
4^3-(1-x)^3 est divisible par par 4-(1-x)
car a^n-b^n est divisible par a-b
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 21 Sep 2012, 19:22
par Luc » 21 Sep 2012, 19:22
titine a écrit:Il faut savoir que :
a^3 + b^3 = (a + b)(a² - ab + b²)
Facile à vérifier en développant.
Un autre identité mais qui revient strictement au même
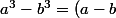(a^2+ab+b^2))
appliquée avec
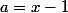
et
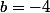
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
