Volvic a écrit: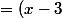(-(x-3)(x+6)))
non pourquoi le - est au début
Arf, car j'ai factorisé par les deux premiers facteurs puis j'ai recopié dans l'ordre...
En prenant les 2eme et troisieme facteurs, mon x disparaît

j’imagine très mal ce résultat comme bon...
Volvic a écrit: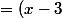(-(x-3)(x+6)))
non pourquoi le - est au début


Lostounet a écrit:Méthode 1: Cendrillon et essayage
Vérifier pour certains x si l'expression de départ et celle de la fin donne pareil. Exemple ici:
(x-3)^2 - (x - 3)(x + 6)
Pour x = 1, cela donne (1 - 3)^2 - (1 - 3)(1 + 6) = 18
Alors que -9(x - 3) donne pour x = 1 -9*(1-3) = 18
Lostounet a écrit:Donc le (-1) ne rentre que dans UNE des deux autres parenthèses:
(-1)*(x + 3)*(x + 4) = (-x - 3)(x + 4) = (x + 3)(-x - 4)
Lostounet a écrit:Pourquoi un moins supprimerait une parenthèse? xD
Avant de faire une manip, pense d'abord au sens de ce que tu fais. Des fois je suis surpris de voir que tu sais vraiment ce que tu fais et des fois tu inventes des trucs qui n'ont pas de senspourquoi
Volvic a écrit:car j'ai retenu qu'on enlève le - devant la parenthèse puis on inverse les signes à l'intérieur, en enlevant la parenthèse xD
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :