Explication simple de la théorie des ensembles
15 messages
- Page 1 sur 1
Explication simple de la théorie des ensembles
Bonjour,
Je ne trouve pas d'explication simple de la construction d'ensembles infinis de plus en plus grands sans fin (Cantor, ...).
Est-ce que c'est dû aux fait qu'on compte les parties des ensembles ou autre chose ou bien cela et autre chose ?
Y a t-il un rapport entre cardinal et parties d'un ensemble ?
Les bases en fait de tout ça : aleph 35 ce serait quoi ?
Merci
Je ne trouve pas d'explication simple de la construction d'ensembles infinis de plus en plus grands sans fin (Cantor, ...).
Est-ce que c'est dû aux fait qu'on compte les parties des ensembles ou autre chose ou bien cela et autre chose ?
Y a t-il un rapport entre cardinal et parties d'un ensemble ?
Les bases en fait de tout ça : aleph 35 ce serait quoi ?
Merci
Re: Explication simple de la théorie des ensembles
Salut,
Déjà, de parler d'ensembles infinis "de plus en plus grand", il faut quand même se méfier : pour les ensembles finis, le concept de "nombre d'éléments" (=cardinal) est quelque chose de très évident et le fait qu'il y ait une bijection (ou une injection ou une surjection) entre deux ensembles finis signifie bien qu'ils ont le même nombre d'éléments (respectivement que le premier en a moins/plus que le deuxième). Mais d'employer ce même vocable de "plus grand" pour les ensembles infinis, si on ne maîtrise pas bien le concept, il faut quand même pas mal se méfier vu que le comportement des cardinaux infinis est assez différent de celui des cardinaux finis. Bref, pour éviter de tout comprendre de travers, il vaut nettement mieux énoncer les choses proprement en disant qu'il existe des ensembles infinis qu'on ne peut pas mettre en bijection les uns avec les autres (et éviter aussi d'utiliser des formules du type "on compte les éléments" dans le cas des ensembles infinis vu que tu risque pas bien de compter grand chose. . . (1)).
Sinon, ce résultat résulte d'un résultat démontré par Georg Cantor qui dit qu'il ne peut pas y avoir de bijection entre un ensemble X et l'ensemble des parties de X (que X soit fini ou pas). Ensuite, en admettant l'axiome du choix, deux ensembles sont toujours "comparables" dans le sens qu'il existe une injection de l'un dans l'autre et quand on prend un ensemble d'ensembles, il y a toujours l'un d'entre eux qui s'injecte dans tout les autres (qui est donc "plus petit" que les autres). Et cela implique qu'on peut ordonner les cardinaux, y compris les cardinaux infinis : le plus petit cardinal infini est noté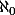 (aleph indice 0), le suivant est
(aleph indice 0), le suivant est 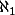 , etc
, etc
En fait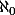 , c'est le cardinal de l'ensemble N entiers naturels. On sait donc que le cardinal de l'ensemble P(N) des parties de N est strictement plus grand que
, c'est le cardinal de l'ensemble N entiers naturels. On sait donc que le cardinal de l'ensemble P(N) des parties de N est strictement plus grand que 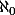 , mais par contre on peut démontrer qu'il n'y a pas suffisamment d'axiomes dans la théorie usuelle des ensembles (ZFC) pour savoir si le cardinal de P(N) c'est
, mais par contre on peut démontrer qu'il n'y a pas suffisamment d'axiomes dans la théorie usuelle des ensembles (ZFC) pour savoir si le cardinal de P(N) c'est 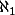 ou
ou 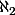 ou
ou 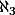 , . . . On peut donc, si on veut, rajouter un axiome à ZFC pour dire que le cardinal de P(N), c'est
, . . . On peut donc, si on veut, rajouter un axiome à ZFC pour dire que le cardinal de P(N), c'est 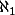 (ça s'apelle l'hypothèse du continu). Si je fait cette remarque concernant l'hypothèse du continu, c'est pour bien montrer que les cardinaux infinis, c'est quelque chose de purement théorique donc il y a pas mal de fait les concernant qui vont dépendre du modèle d'axiomes que l'on pose au départ, par exemple si on ne prend pas l'axiome du choix, on risque d'avoir des ensembles infinis non comparables (aucun des deux n'a "plus d'élément" que l'autre)
(ça s'apelle l'hypothèse du continu). Si je fait cette remarque concernant l'hypothèse du continu, c'est pour bien montrer que les cardinaux infinis, c'est quelque chose de purement théorique donc il y a pas mal de fait les concernant qui vont dépendre du modèle d'axiomes que l'on pose au départ, par exemple si on ne prend pas l'axiome du choix, on risque d'avoir des ensembles infinis non comparables (aucun des deux n'a "plus d'élément" que l'autre)
(1) Sauf Chuck Norris qui a réussi à compter jusqu'à l'infini . . . deux fois . . .
Déjà, de parler d'ensembles infinis "de plus en plus grand", il faut quand même se méfier : pour les ensembles finis, le concept de "nombre d'éléments" (=cardinal) est quelque chose de très évident et le fait qu'il y ait une bijection (ou une injection ou une surjection) entre deux ensembles finis signifie bien qu'ils ont le même nombre d'éléments (respectivement que le premier en a moins/plus que le deuxième). Mais d'employer ce même vocable de "plus grand" pour les ensembles infinis, si on ne maîtrise pas bien le concept, il faut quand même pas mal se méfier vu que le comportement des cardinaux infinis est assez différent de celui des cardinaux finis. Bref, pour éviter de tout comprendre de travers, il vaut nettement mieux énoncer les choses proprement en disant qu'il existe des ensembles infinis qu'on ne peut pas mettre en bijection les uns avec les autres (et éviter aussi d'utiliser des formules du type "on compte les éléments" dans le cas des ensembles infinis vu que tu risque pas bien de compter grand chose. . . (1)).
Sinon, ce résultat résulte d'un résultat démontré par Georg Cantor qui dit qu'il ne peut pas y avoir de bijection entre un ensemble X et l'ensemble des parties de X (que X soit fini ou pas). Ensuite, en admettant l'axiome du choix, deux ensembles sont toujours "comparables" dans le sens qu'il existe une injection de l'un dans l'autre et quand on prend un ensemble d'ensembles, il y a toujours l'un d'entre eux qui s'injecte dans tout les autres (qui est donc "plus petit" que les autres). Et cela implique qu'on peut ordonner les cardinaux, y compris les cardinaux infinis : le plus petit cardinal infini est noté
En fait
(1) Sauf Chuck Norris qui a réussi à compter jusqu'à l'infini . . . deux fois . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Explication simple de la théorie des ensembles
Salut,
C'est surtout les définitions précises qui manquent aux non spécialistes comme moi : la différence entre l'ensemble N et ℵ0 c'est quoi ?
Ou encore plus basiquement : la différence entre le nombre des éléments d'un ensemble et le cardinal de cet ensemble (le nombre d'éléments de ce cardinal).
Mais les ℵ3, ℵ4, ......, , ℵ6777978, etc .... : je ne vois pas à quoi ça peut correspondre ...
Je pense comprendre par rapport aux parties d'un ensemble qui sont en nombres plus grands que les éléments de cet ensemble donc P(N) < P(P(N)) < P(P(P(N))) etc ... : ça ce sont bien des infinis plus hauts, plus larges sans fin, non ?
C'est surtout les définitions précises qui manquent aux non spécialistes comme moi : la différence entre l'ensemble N et ℵ0 c'est quoi ?
Ou encore plus basiquement : la différence entre le nombre des éléments d'un ensemble et le cardinal de cet ensemble (le nombre d'éléments de ce cardinal).
Mais les ℵ3, ℵ4, ......, , ℵ6777978, etc .... : je ne vois pas à quoi ça peut correspondre ...
Je pense comprendre par rapport aux parties d'un ensemble qui sont en nombres plus grands que les éléments de cet ensemble donc P(N) < P(P(N)) < P(P(P(N))) etc ... : ça ce sont bien des infinis plus hauts, plus larges sans fin, non ?
Re: Explication simple de la théorie des ensembles
Les cardinaux infinis (donc les alephs), il y a plusieurs définitions possibles : soit on dit que c'est des classes d'ensembles via la relation d'équivalence "être en bijection avec", mais dans ce cas là, un cardinal, ce n'est pas un ensemble (dans la théorie des ensemble, un "ramassis" quelconque d'ensembles n'est pas forcément un ensemble, vu que sinon, on tomberais immédiatement sur le paradoxe de Russel). Soit on dit qu'un cardinal, c'est un ordinal particulier (cherche sur wiki ce qu'est un ordinal) et dans ce cas, les cardinaux sont bien des ensembles (très particuliers) et le premier cardinal infini c'est à dire 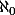 , c'est exactement l'ensemble des entiers naturels (où 0 c'est l'ensemble vide, 1 c'est {0}, 2 c'est {0,1}, etc . . .).
, c'est exactement l'ensemble des entiers naturels (où 0 c'est l'ensemble vide, 1 c'est {0}, 2 c'est {0,1}, etc . . .).
Ensuite, la différence entre "le nombre d'éléments" et "le cardinal", là, c'est facile : pour les ensembles finis, c'est exactement la même chose et, pour les ensembles infinis, la notion de "nombre d'élément" n'a aucun sens (vu qu'il n'existe évidement aucun nombre infini) alors qu'on peut donner un sens à la notion de cardinal (c.f. çi dessus : soit c'est une classe d'ensembles pouvant être mis en bijection, soit c'est un ordinal particulier).
Enfin, etc, comme je te l'ai déjà dit, c'est "les suivant" de
etc, comme je te l'ai déjà dit, c'est "les suivant" de 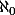 et sans axiome suplémentaire dans ZFC, on ne peut pas dire grand chose de qui c'est : en fait, ça peut être un peu n'importe quoi et on peut, par exemple, supposer que
et sans axiome suplémentaire dans ZFC, on ne peut pas dire grand chose de qui c'est : en fait, ça peut être un peu n'importe quoi et on peut, par exemple, supposer que 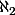 c'est le cardinal de P(N), que
c'est le cardinal de P(N), que 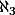 c'est celui de P(P(N)) etc . . . ça s'appelle "l'hypothèse du continu généralisée" et on sait que, si ZFC n'est pas contradictoire, alors ZFC + HGC (hypothèse du continu généralisée) n'est pas contradictoire non plus.
c'est celui de P(P(N)) etc . . . ça s'appelle "l'hypothèse du continu généralisée" et on sait que, si ZFC n'est pas contradictoire, alors ZFC + HGC (hypothèse du continu généralisée) n'est pas contradictoire non plus.
Ensuite, la différence entre "le nombre d'éléments" et "le cardinal", là, c'est facile : pour les ensembles finis, c'est exactement la même chose et, pour les ensembles infinis, la notion de "nombre d'élément" n'a aucun sens (vu qu'il n'existe évidement aucun nombre infini) alors qu'on peut donner un sens à la notion de cardinal (c.f. çi dessus : soit c'est une classe d'ensembles pouvant être mis en bijection, soit c'est un ordinal particulier).
Enfin,
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Explication simple de la théorie des ensembles
Ok, si on fait abstraction de tout autre nombre que ceux de l'ensemble N (pas de Z, D, R, ....) la seule chose qui puisse dépasser N c'est de prendre en considération les parties de N.
C'est bien cela ?
C'est bien cela ?
Re: Explication simple de la théorie des ensembles
Ben justement, ça dépend des axiomes que l'on prend : il faut bien comprendre que tout ça (à savoir les ensembles infinis),c'est du "pur théorique" vu qu'il n'y a rien dans le monde concret qui est infini.
Donc ce "monde des ensembles infinis" est totalement imaginaire et les propriétés des cardinaux infinis qu'on va avoir vont dépendre des hypothèses que l'on fait sur ce "monde imaginaire", (c'est ce qu'on appelle des axiomes en math). Les axiomes qu'une grande majorité de mathématiciens prennent pour décrire ce "monde imaginaire", c'est les axiome de Zermelo-Fraenkel (ZF) qui permettent de démontrer une bonne partie des résultats qui sont "intuitivement vrais" (et qui était utilisés par les matheux bien avant qu'on modélise les maths via un système d'axiomes). Assez souvent on rajoute l'axiome du choix (ce qui donne ZFC) vu que certains résultats un peu techniques ne peuvent être démontré avec les seuls axiomes de ZF. Mais déjà, cet axiome du choix permet aussi de démontrer des résultat plus que bizarre au niveau intuitif comme le paradoxe de Banach-Tarski (on peut couper une boule en un nombre fini de morceaux et, avec les morceaux, reconstituer deux boules de la même taille que celle de départ . . .) donc certains matheux préfèrent éviter d'utiliser cet axiome. Sauf que, si on ne prend pas cet axiome, ben concernant la théorie des cardinaux, on ne peut plus faire grand chose vu qu'il risque d'exister des ensembles non comparables (pas d'injection du premier dans le second ni du second dans le premier) ce qui signifie que la notion d'ensemble "plus gros" qu'un autre ensemble n'a plus de sens.
Et concernant ta question,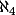 .
.
Bref, P(N) "dépasse" forcément N, mais par contre, dans le modèle classique (ZFC), on ne peut pas démontrer, ni infirmer que c'est lui le "suivant" : c'est un résultat indécidable de ZFC.
Donc ce "monde des ensembles infinis" est totalement imaginaire et les propriétés des cardinaux infinis qu'on va avoir vont dépendre des hypothèses que l'on fait sur ce "monde imaginaire", (c'est ce qu'on appelle des axiomes en math). Les axiomes qu'une grande majorité de mathématiciens prennent pour décrire ce "monde imaginaire", c'est les axiome de Zermelo-Fraenkel (ZF) qui permettent de démontrer une bonne partie des résultats qui sont "intuitivement vrais" (et qui était utilisés par les matheux bien avant qu'on modélise les maths via un système d'axiomes). Assez souvent on rajoute l'axiome du choix (ce qui donne ZFC) vu que certains résultats un peu techniques ne peuvent être démontré avec les seuls axiomes de ZF. Mais déjà, cet axiome du choix permet aussi de démontrer des résultat plus que bizarre au niveau intuitif comme le paradoxe de Banach-Tarski (on peut couper une boule en un nombre fini de morceaux et, avec les morceaux, reconstituer deux boules de la même taille que celle de départ . . .) donc certains matheux préfèrent éviter d'utiliser cet axiome. Sauf que, si on ne prend pas cet axiome, ben concernant la théorie des cardinaux, on ne peut plus faire grand chose vu qu'il risque d'exister des ensembles non comparables (pas d'injection du premier dans le second ni du second dans le premier) ce qui signifie que la notion d'ensemble "plus gros" qu'un autre ensemble n'a plus de sens.
Et concernant ta question,
c'est pas franchement ça. Ce qui est systématiquement vrai (dans ZF), c'est qu'il existe une injection mais pas de bijection de N dans P(N). Dit avec des mots imagés (qui peuvent prêter à confusion), cela signifie que N et P(N) sont forcément comparables (alors que sans l'axiome du choix il peut exister des ensembles non comparables), et que P(N) est forcément "plus gros" que N. Par contre, est ce que P(N) et "le suivant" de N, c'est à dire est-ce que c'est le "plus petit" ensemble strictement "plus gros" que N, ben là, il n'y a pas de réponse dans ZF, ni dans ZFC : on n'a pas assez d'hypothèses concernant le "monde imaginaire" des ensembles infinis pour pouvoir répondre à cette question. Donc on peut, si on veut, rajouter comme hypothèse concernant notre "monde imaginaire" que P(N) est bien le "suivant" de N. Mais on peut bien sûr aussi rajouter comme hypothèse que, dans notre "monde imaginaire" P(N) ce n'est pas le "suivant" de N, mais, par exemple, le suivant du suivant du suivant c'est à diremarcheur a écrit:la seule chose qui puisse dépasser N c'est de prendre en considération les parties de N.
Bref, P(N) "dépasse" forcément N, mais par contre, dans le modèle classique (ZFC), on ne peut pas démontrer, ni infirmer que c'est lui le "suivant" : c'est un résultat indécidable de ZFC.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Explication simple de la théorie des ensembles
Ok, mais ma question était plus générale, à savoir par ex :
est-ce que ''le plus petit nombre au delà de N'' (donc sûrement que cela s'écrit N + 1), est-ce que ça c'est sans considération au fait qu'il y a des parties de N. Je veux dire : autre chose.
En aussi d'une manière générale encore : peut-on parler de cardinaux ou d'ordinaux sans faire appel à une quelconque notion de parties concernant les ensembles ?
est-ce que ''le plus petit nombre au delà de N'' (donc sûrement que cela s'écrit N + 1), est-ce que ça c'est sans considération au fait qu'il y a des parties de N. Je veux dire : autre chose.
En aussi d'une manière générale encore : peut-on parler de cardinaux ou d'ordinaux sans faire appel à une quelconque notion de parties concernant les ensembles ?
Re: Explication simple de la théorie des ensembles
Là, ce que tu fait, c'est justement ce que je disait dans mon premier message, c'est à dire qu'à force de voir des trucs simplifiés concernant les cardinaux, tu fait comme si ils se comportaient tous comme les cardinaux finis (i.e. les nombres entiers) et ça :
ça ne veut évidement rien dire : N c'est un cardinal non fini donc ce n'est pas un nombre, mais un objet très théorique qui vit dans notre fameux "monde imaginaire des mathématiques" (axiomatisées) et le "suivant" au sens des cardinaux (qui ne se note pas N+1, qui, lui serait plutôt le suivant au sens des ordinaux), ben ça fait 3 fois que je te le dit : dans l'axiomatique de ZF ou de ZFC, vu les seules hypothèses qu'on a fait sur notre monde imaginaire, ben on ne peut pas savoir qui c'est. Dit autrement, parmi les différents mondes imaginaires vérifiant les axiomes de ZFC, dans certains d'entre eux, le suivant de N, ça va être P(N), mais pas dans tous. Et je t'ai déjà aussi écrit dans un message précédent que dans la théorie des cardinaux, tout ce qu'on sait, c'est que P(X) (X ensemble quelconque) est toujours "strictement plus gros" que X ce qui montre principalement qu'il existe des ensembles infinis "de plus en plus gros"marcheur a écrit:Ok, mais ma question était plus générale, à savoir par ex :
est-ce que ''le plus petit nombre au delà de N'' (donc sûrement que cela s'écrit N + 1), est-ce que ça c'est sans considération au fait qu'il y a des parties de N.
Je t'ai donné (1er message) les définitions usuelle de ce que sont les cardinaux. Y voit-tu une référence à l'ensemble des parties d'un ensemble donné ?marcheur a écrit:En aussi d'une manière générale encore : peut-on parler de cardinaux ou d'ordinaux sans faire appel à une quelconque notion de parties concernant les ensembles ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Explication simple de la théorie des ensembles
Ok, c'était juste pour être sûr de bien comprendre le rapport ou le non rapport entre ensembles et nombres.
Moi mon domaine c'est la philo et j'ai déjà pas mal réfléchi à un tas de choses comme ça dont l'infini et c'est évident pour moi qu'il n'y a pas de nombre infini.
Et pourtant dans des écrits directs de Cantor il y a bien ces mots ''nombre infini'' : je pense que c'est une erreur de traduction.
Moi mon domaine c'est la philo et j'ai déjà pas mal réfléchi à un tas de choses comme ça dont l'infini et c'est évident pour moi qu'il n'y a pas de nombre infini.
Et pourtant dans des écrits directs de Cantor il y a bien ces mots ''nombre infini'' : je pense que c'est une erreur de traduction.
Re: Explication simple de la théorie des ensembles
Je tiens aussi à dire que je ne me contente pas de questionner dans un forum mais que je cherche à comprendre tout ça en faisant de nombreuses recherches.
Par exemple ici, on peut penser qu'il n'y a pas de cardinaux infinis qui ne fassent appel à la notion de ''parties d'ensemble (s)'' :
https://uel.unisciel.fr/mathematiques/l ... h9_06.html
Par exemple ici, on peut penser qu'il n'y a pas de cardinaux infinis qui ne fassent appel à la notion de ''parties d'ensemble (s)'' :
https://uel.unisciel.fr/mathematiques/l ... h9_06.html
Re: Explication simple de la théorie des ensembles
Je viens de regarder le laïus en question et je ne comprend pas ce que tu veut dire par "qui ne font pas appel à". Ce que dit le bidule, ben c'est ce que je t'ai dit précédemment, c'est à dire que le fait que P(X) est "strictement plus gros" que X implique évidement qu'il existe des cardinaux infinis de plus en plus grand. Mais ce n'est bien évidement pas parce qu'on utilise ce fait (que P(X) est > X) que ça veut dire qu'on a besoin de la notion "ensemble des parties" pour définir les cardinaux.marcheur a écrit:Par exemple ici, on peut penser qu'il n'y a pas de cardinaux infinis qui ne fassent appel à la notion de ''parties d'ensemble (s)''
Est ce que, du fait que pour démontrer que l'ensemble des entiers naturels est infini on utilise (par exemple) le fait que pour tout entier N, l'entier N+1 est strictement plus grand que N cela signifie pour toi que "il n'y a pas d'entiers qui ne fasse pas appel à la notion d'addition d'une unité" ?
(moi j'ai pas la réponse vu que je comprend pas ce que tu veut dire par "faire appel à" dans ce contexte)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Explication simple de la théorie des ensembles
Ce que j'entends par ''faire appel à'' c'est : ''se servir de ces concepts là obligatoirement'', ici : du concept de partie d'un ensemble.
La notion de ''partie d'un ensemble'' est une construction mathématique qui n'a rien d'évident.
Dans ce dernier exemple je ne parlais pas de cardinaux simplement mais de cardinaux infinis.
Et donc ici précisément : qui dit ''cardinaux infinis'' dit ''parties des ensembles''.
Si ce n'est pas le cas, il me faudrait donc un exemple de cardinaux infinis où on n'a pas besoin de ça, où on ne s'en sert pas (où il suffit de la notion de bijection ou autre chose par ex).
La notion de ''partie d'un ensemble'' est une construction mathématique qui n'a rien d'évident.
Dans ce dernier exemple je ne parlais pas de cardinaux simplement mais de cardinaux infinis.
Et donc ici précisément : qui dit ''cardinaux infinis'' dit ''parties des ensembles''.
Si ce n'est pas le cas, il me faudrait donc un exemple de cardinaux infinis où on n'a pas besoin de ça, où on ne s'en sert pas (où il suffit de la notion de bijection ou autre chose par ex).
Re: Explication simple de la théorie des ensembles
Je ne comprend toujours pas franchement la question . . .
Pour définir l'ensemble N des entiers naturels (qui est bien un cardinal infini), il n'y a nul besoin de se référer à l'ensemble des parties de quoi que ce soit. Et si on construit par exemple l'ensemble des réels via les coupures de Dedekind sur les quotients, il n'y a pas besoin non plus d'utiliser l'ensemble de toutes les parties d'un ensemble donné. Et on peut ensuite démontrer que ces deux ensembles N et R ne sont pas en bijections l'un avec l'autre donc qu'ils définissent deux cardinaux différents (au sens de la première définition).
Et sinon, concernant le fait que "la construction de l'ensemble des parties est un concept qui n'a rien d'évident" en ce qui me concerne, c'est pas franchement ça que je ne trouve "pas évident" dans cet histoire de cardinaux, mais plutôt la notion de système axiomatisé qu'il faut un minimum maîtriser si on veut comprendre les résultat du type "l'hypothèse du continu est indécidable dans ZFC"
Pour définir l'ensemble N des entiers naturels (qui est bien un cardinal infini), il n'y a nul besoin de se référer à l'ensemble des parties de quoi que ce soit. Et si on construit par exemple l'ensemble des réels via les coupures de Dedekind sur les quotients, il n'y a pas besoin non plus d'utiliser l'ensemble de toutes les parties d'un ensemble donné. Et on peut ensuite démontrer que ces deux ensembles N et R ne sont pas en bijections l'un avec l'autre donc qu'ils définissent deux cardinaux différents (au sens de la première définition).
Et sinon, concernant le fait que "la construction de l'ensemble des parties est un concept qui n'a rien d'évident" en ce qui me concerne, c'est pas franchement ça que je ne trouve "pas évident" dans cet histoire de cardinaux, mais plutôt la notion de système axiomatisé qu'il faut un minimum maîtriser si on veut comprendre les résultat du type "l'hypothèse du continu est indécidable dans ZFC"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Explication simple de la théorie des ensembles
Ok.
Mais dans les maths il y a des notions qui sont plus évidentes et moins de type ''pure construction mathématique'' que d'autres.
La simple notion d'infini n'est pas en elle-même une pure construction des maths (même au sens purement quantitatif) contrairement à celle de parties d'ensembles ou de bijection , et autres.
Depuis quelques semaines j'essaye de lire (en traduction) plein d'articles sur le rapport entre mathématiques, philosophie et théologie sur la notion d'infini sur ce site : https://www.academia.edu/
Mais dans les maths il y a des notions qui sont plus évidentes et moins de type ''pure construction mathématique'' que d'autres.
La simple notion d'infini n'est pas en elle-même une pure construction des maths (même au sens purement quantitatif) contrairement à celle de parties d'ensembles ou de bijection , et autres.
Depuis quelques semaines j'essaye de lire (en traduction) plein d'articles sur le rapport entre mathématiques, philosophie et théologie sur la notion d'infini sur ce site : https://www.academia.edu/
Re: Explication simple de la théorie des ensembles
L'infini en mathématique, pendant très longtemps, ça a été totalement "tabou" vu le nombre de paradoxe auquel ça conduisait et il a fallu attendre Cantor (donc très récent) pour que quelqu'un ose tenter de la manipuler en temps qu'infini actuel et pas simplement d'infini potentiel, sauf que si on le manipule "n'importe comment" (i.e. plus ou moins au sens naïf), ben ça conduit immédiatement à de belle contradictions (par exemple le paradoxe de Russell). Donc,non, l'infini (mathématique), ce n'est absolument pas du tout une notion simple qu'on peut ne serait ce vaguement appréhender proprement avec un point de vue naïf dessus.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
15 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
