Exo sur les expos
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 19 Nov 2005, 15:37
par Anonyme » 19 Nov 2005, 15:37
salut j'aurais besoin d'un petit coup de main pour mon exo, voici ce que j'ai :
On note f(x) la fonction définie sur |R par :
f(x)= (2+cos(x)-sin(x))e1-x
1°a) Déterminer le signe de f(x)
1°b) Démontrer que f est strictement décroissante sur |R.
J'ai déjà calculé la dérivée, mais je suis pas sûr qu'elle soit correcte, donc faudrait que qlq1 puisse me "valider" ceci :
f'(x)= -2sin(x)e^(1-x) + 2e^(1-x) / (e(1-x))^2
Ensuite je vois pas comment mis prendre, si on pouvait me guider plz
d'avance merci à celui qui m'apportera son aide :)
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 15:46
par becirj » 19 Nov 2005, 15:46
Bonjour
D'accord pour la dérivée. En mettant

en facteur au numérateur, le signe est facile à étudier car

-
Anonyme
 par Anonyme » 19 Nov 2005, 15:51
par Anonyme » 19 Nov 2005, 15:51
oki merci ça me rassure je suis pas si nul :)
donc normalement le signe doit être ' - '
mais après comment je démontre que f est strictement décroissante sur |R ? stp
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 15:59
par becirj » 19 Nov 2005, 15:59
Problème : la fonction est strictement croissante (sa dérivée est positive).
Où est l'erreur ? Dans la fonction que tu as recopiée ou dans le texte de la question ?
-
Anonyme
 par Anonyme » 19 Nov 2005, 16:01
par Anonyme » 19 Nov 2005, 16:01
c'est bien dit démontrer que f est strictement décroissante sur R
ou est l erreur? ma dérivée?
-
Anonyme
 par Anonyme » 19 Nov 2005, 16:03
par Anonyme » 19 Nov 2005, 16:03
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 16:06
par becirj » 19 Nov 2005, 16:06
Dans ton texte, j'avais lu qu'il s'agissait d'un quotient or il s'agit d'un produit. Les calculs sont à recommencer !
-
Anonyme
 par Anonyme » 19 Nov 2005, 16:08
par Anonyme » 19 Nov 2005, 16:08
j'ai utilisé : u'v - v'u / v² (où u = (2+cos(x)-sin(x))
ca marche pas?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 16:15
par becirj » 19 Nov 2005, 16:15
Il s'agit de la dérivée d'un produit :
'=u'v+uv')
avec
=2+\cos x -\sin x)
et
=e^{1-x})
-
Anonyme
 par Anonyme » 19 Nov 2005, 16:16
par Anonyme » 19 Nov 2005, 16:16
evidemment si je prend pas la bonne formule...
je suis vraiment à la masse défois...
bon je vais refaire le calcul, merci
-
Anonyme
 par Anonyme » 19 Nov 2005, 16:25
par Anonyme » 19 Nov 2005, 16:25
bon une fois modifié j'obtiens f'(x)= -2e^1-x
donc ensuite je fais -2e^1-x < 0 c'est bien ca ?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 16:32
par becirj » 19 Nov 2005, 16:32
Non
= (-\sin x-\cos x)e^{1-x}+(-e^{1-x})(2+\cos x - \sin x)=e^{1-x}(-\sin x -\cos x -2-\cos x+\sin x)=e^{1-x}(-2-2\cos x) =-2e^{1-x}(1+\cos x))
-
Anonyme
 par Anonyme » 19 Nov 2005, 16:36
par Anonyme » 19 Nov 2005, 16:36
d'accord .
-
Anonyme
 par Anonyme » 19 Nov 2005, 17:06
par Anonyme » 19 Nov 2005, 17:06
ensuite j'ai fait ca :
-1 < cos x < 1
0 < cos x +1 < 2
-2e^1-x (cosx +1) < 2 x -2e^1-x
soit -2e^1-x (cosx +1) < -4e^1-x
donc le signe de f(x) est négatif
comment je démontre que c'est strictement décroissant??
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 18:26
par becirj » 19 Nov 2005, 18:26
Attention, il y a une faute, tu as multiplié une inégalité par -

qui est négatif donc l'inégalité change de sens. IL suffit d'écrire

et -

donc leur produit est inférieur ou égal à 0 soit
\leq 0)
La dérivée peut être nulle lorsque
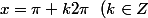)
mais elle ne s'annule que pour des valeurs isolées donc la fonction f est strictement décroissante.
-
Anonyme
 par Anonyme » 19 Nov 2005, 20:34
par Anonyme » 19 Nov 2005, 20:34
oki merci!
juste une chose tu entends quoi par "valeurs isolées" ?
-
becirj
- Membre Rationnel
- Messages: 698
- Enregistré le: 16 Oct 2005, 08:56
-
 par becirj » 19 Nov 2005, 22:39
par becirj » 19 Nov 2005, 22:39
La fonction ne serait pas strictement croissante si elle était nulle sur un intervalle non vide de R (elle serait seulement croissante) mais ici ce n'est pas le cas car les nombres

sont séparés et ne constituent pas un intervalle.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 110 invités
 qui est négatif donc l'inégalité change de sens. IL suffit d'écrire
qui est négatif donc l'inégalité change de sens. IL suffit d'écrire  et -
et - donc leur produit est inférieur ou égal à 0 soit
donc leur produit est inférieur ou égal à 0 soit \leq 0)
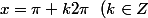) mais elle ne s'annule que pour des valeurs isolées donc la fonction f est strictement décroissante.
mais elle ne s'annule que pour des valeurs isolées donc la fonction f est strictement décroissante.