Exo de probabilités
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 14:09
par yayamat » 29 Mar 2015, 14:09
salut à tous je dois faire cet exo pour ce vendredi..j'etais absent au cours.
merci
Soit n un nombre entier.
On considère une variable aléatoire X dont la loi est donnée par le tableau suivant:
xi 1 2 3 ... n
P(X=xi) 1/n 1/n ... 1/n
1)Vérifier que ce tableau est bien celui d'une loi de probabilité.
2)Calculer E(x) n
3)a)Montrer que E((k+1)^3-k^3)=n^3+3n^2+3n (info:E c'est la symbole somme)
k=1
n n
b)Montrer que E((k+1)^3-k^3)=3 E k^2+(3n2+5n)/2
k=1 k=1
n
C)en déduire que E k^2=(n(n+1)(2n+1))/6
k=1
D)Calcumer V(X)
4)Un urne contient 50jétonq numérotés de 1à50.On tire au hasard un jeton et on note X ce numéro.Calculer E(X) et V(X).
______________________
1)la loi de probabilité c'est déterminer la probabilité de chacunes des issues.
donc 1/n+1/n+1/n+...+1/n=1. c'est tout? merci
maintenant je fais le question 2
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 14:11
par yayamat » 29 Mar 2015, 14:11
xi 1 2 3 ... n
P(X=xi) 1/n 1/n 1/n ... 1/n
excuse moi j'ai fais une petite erreur.
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 14:53
par Shew » 29 Mar 2015, 14:53
yayamat a écrit:xi 1 2 3 ... n
P(X=xi) 1/n 1/n 1/n ... 1/n
excuse moi j'ai fais une petite erreur.
Si un tableau représente une loi de probabilité alors chaque élement est un nombre compris entre 0 et 1 et la somme totale des probabilités vaut 1 .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 14:55
par yayamat » 29 Mar 2015, 14:55
Shew a écrit:Si un tableau représente une loi de probabilité alors chaque élement est un nombre compris entre 0 et 1 et la somme totale des probabilités vaut 1 .
oui justmement je cite "P(X=xi)=1 1/n+1/n+1/n+...+1/n "??
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 14:58
par Shew » 29 Mar 2015, 14:58
yayamat a écrit:oui justmement je cite "P(X=xi)=1 1/n+1/n+1/n+...+1/n "??
Il faut être un peu plus précis en constatant qu'il y'a n éléments dans le tableau .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 15:04
par yayamat » 29 Mar 2015, 15:04
Shew a écrit:Il faut être un peut plus précis en constatant qu'il y'a n éléments dans le tableau .
omega : ( 1;2;3;...;n ) ou les valeurs prises par X sont ( 1;2;3;...;n )
n
E(la symbole de somme) p=1
i=1
donc oui ce tableau est bien celui d'une loi de probabilité..
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 15:09
par Shew » 29 Mar 2015, 15:09
yayamat a écrit:omega : ( 1;2;3;...;n ) ou les valeurs prises par X sont ( 1;2;3;...;n )
n
E(la symbole de somme) p=1
i=1
donc oui ce tableau est bien celui d'une loi de probabilité..
Chaque élément

a une probabilité de 1/n d'apparaitre , il y'a donc equiprobabilité . n > 1 donc

et il y'a n éléments au total soit :

. Ce tableau suit bien une loi de probabilité .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 15:15
par yayamat » 29 Mar 2015, 15:15
Shew a écrit:Chaque élément

a une probabilité de 1/n d'apparaitre , il y'a donc equiprobabilité . n > 1 donc

et il y'a n éléments au total soit :

. Ce tableau suit bien une loi de probabilité .
ah oui je n'avais pas pensé que les issues de X sont equiprobables!
merci beaucoup
2)
E(X)=1*1/n +2*1/n +3*1/n +...+n*1/n = 1/n + 2/n + 3/n + n/n = 6/n + n/n =6n/n=6
je doute que je fais une petite erreur
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 15:19
par Shew » 29 Mar 2015, 15:19
yayamat a écrit:ah oui je n'avais pas pensé que les issues de X sont equiprobables!
merci beaucoup
2)
E(X)=1*1/n +2*1/n +3*1/n +...+n*1/n = 1/n + 2/n + 3/n + n/n = 6/n + n/n =6n/n=6
je doute que je fais une petite erreur
La question 2 n'est pas complète je crois
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 15:37
par yayamat » 29 Mar 2015, 15:37
Shew a écrit:La question 2 n'est pas complète je crois
... est remplacé par K ?
E(X)=1
donc 1 1*1/n + 2*1/n + 3*1/n + K*1/n + n*1/n
:mur:
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 16:02
par yayamat » 29 Mar 2015, 16:02
y'a personne ? up
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 16:06
par Shew » 29 Mar 2015, 16:06
yayamat a écrit:... est remplacé par K ?
E(X)=1
donc 1 1*1/n + 2*1/n + 3*1/n + K*1/n + n*1/n
:mur:
Je n'ai pas compris que voulez vous dire ???
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 16:14
par yayamat » 29 Mar 2015, 16:14
Shew a écrit:Je n'ai pas compris que voulez vous dire ???
il faut que je calcule E(X)
peut-être je fais n'importe quoi..
pour la deuxième question,
E(X)=1*1/n +2*1/n +3*1/n +...+n*1/n=1/n + 2/n +3/n +...+1= ??
"..."je ne sais pas quoi faire
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 16:48
par yayamat » 29 Mar 2015, 16:48
1+2+...+n= n(n+1)/2 c'est la suite d'arithmétique ?!
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 16:57
par Shew » 29 Mar 2015, 16:57
yayamat a écrit:1+2+...+n= n(n+1)/2 c'est la suite d'arithmétique ?!
Plutot :
 = 1*\frac{1}{n} + 2*\frac{1}{n} + 3*\frac{1}{n} + ... + n*\frac{1}{n} = \frac{1}{n}(1 + 2 + 3 + ... + n) = \frac{1}{n}*\sum_{k = 1}^n (k))
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 17:16
par yayamat » 29 Mar 2015, 17:16
Shew a écrit:Plutot :
 = 1*\frac{1}{n} + 2*\frac{1}{n} + 3*\frac{1}{n} + ... + n*\frac{1}{n} = \frac{1}{n}(1 + 2 + 3 + ... + n) = \frac{1}{n}*\sum_{k = 1}^n (k))
Ah d'accord merci beaucoup.
pour la question 3)
E((k+1)^3-k^3)=n^2+3n^2+3n
=>E((k+1)^3-k^3)
=(k^3+3*k^2*1+1^3)-k^3
=3k^2+1
non pas ca je ne sais pas..
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 17:21
par Shew » 29 Mar 2015, 17:21
yayamat a écrit:Ah d'accord merci beaucoup.
pour la question 3)
E((k+1)^3-k^3)=n^2+3n^2+3n
=>E((k+1)^3-k^3)
=(k^3+3*k^2*1+1^3)-k^3
=3k^2+1
non pas ca je ne sais pas..
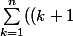^3 - k^3) = [(1 + 1)^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3])
. Recherchez les expressions communes et simplifiez
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 17:41
par yayamat » 29 Mar 2015, 17:41
Shew a écrit: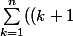^3 - k^3) = [(1 + 1)^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3])
. Recherchez les expressions communes et simplifiez
=(8-1)+(27-8)+(64-27)+...+(n^3+3*n^2*1+3*n*1+1^3)-n^3)
=7+19+37+...+(n^3+3n^2+3n+1-n^3)
=63+...+3n^2+3n+1
pourtant je n'ai pas trouvé les expressions communes..
-
Shew
- Membre Irrationnel
- Messages: 1394
- Enregistré le: 02 Jan 2011, 14:39
-
 par Shew » 29 Mar 2015, 17:45
par Shew » 29 Mar 2015, 17:45
yayamat a écrit:=(8-1)+(27-8)+(64-27)+...+(n^3+3*n^2*1+3*n*1+1^3)-n^3)
=7+19+37+...+(n^3+3n^2+3n+1-n^3)
=63+...+3n^2+3n+1
pourtant je n'ai pas trouvé les expressions communes..
Prenons la première somme
^3 - 1^3] + [(2 + 1)^3 - 2^3])
on constate que
^3 = 2^3)
soit

. Essayez de raisonner de façon analogue et de trouver un schema systématique qui se répète sans écrire toutes les expressions (ce serait interminable) .
-
yayamat
- Membre Naturel
- Messages: 46
- Enregistré le: 12 Mar 2013, 18:21
-
 par yayamat » 29 Mar 2015, 17:57
par yayamat » 29 Mar 2015, 17:57
Shew a écrit:Prenons la première somme
^3 - 1^3] + [(2 + 1)^3 - 2^3])
on constate que
^3 = 2^3)
soit

. Essayez de raisonner de façon analogue et de trouver un schema systématique qui se répète sans écrire toutes les expressions (ce serait interminable) .
\sum_{k = 1}^n ((k + 1)^3 - k^3) = [(1 + 1)^3 - 1^3] + [(2 + 1)^3 - 2^3] + [(3 + 1)^3 - 3^3] + ... + [(n + 1)^3 - n^3]
=((1 + 1)^3 - 1^3) + ((2 + 1)^3 - 2^3)+((3+1)^3-3^3)+((n+1)^3-n^3)
=(2^3-1^3)+(3^3-2^3)+(4^3-3^3)+((n+1)^3-n^3)
=1^3+1^3+1^3+...+((n+1)^3-n^3)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
a une probabilité de 1/n d'apparaitre , il y'a donc equiprobabilité . n > 1 donc
et il y'a n éléments au total soit :
. Ce tableau suit bien une loi de probabilité .
on constate que
soit
. Essayez de raisonner de façon analogue et de trouver un schema systématique qui se répète sans écrire toutes les expressions (ce serait interminable) .
