[1éreS] Exerices de maths, divers

[potterboy6274]

Bonjour donc je me presente je m'appele james et je suis en 1ére S voila mon soucis, ma prof de maths ma donner aujourd'hui un dm d'une dizaine d'exercise, sur ces dix exercies il y en a malheuresement 2 que je n'arrive pas a realiser, donc si vous pouvez m'aider ce serai super sympa de votre part car ayant des tas de controles et dm cette semaine je ne m'ensort as avec ce ryhme.
Ci joint les deux exercices, merci d'avance.

[abcd22]

Pour le 83, on peut exprimer MN et MQ en fonction de a et x (tan(Pi/3)=QM/AM). On a donc l'aire du rectangle en fonction de a et x et il faut étudier la fonction (de x) sur [0,a] pour trouver où elle admet un maximum.

[potterboy6274]

Merci, mais pour tout te dire je ne comprend pas top ce que tu dit, je sais j'ai d'enorme difficulté en maths, j'en ai pas eu en seconde a cause d'un prof absent .... :triste: :triste: :triste:
:cry: :cry: le dm est pour jeudi, je sais pas coment je vasi faire... Aidez moi svp... :cry: :cry:

[potterboy6274]

Aider moi je vous en prie ..............

[abcd22]

MN=a-2x (AM = NB car le triangle ABC est équilatéral)
Le triangle AMQ est rectangle en M, donc , et comme ABC est équilatéral, degrés, donc . On a donc .
L'aire du rectangle vaut
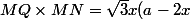Il reste à étudier cette fonction (de x, a est constant) pour trouver où elle admet un maximum.

[fonfon]

Salut,
f(x)=cos(2x-pi/6)

1a) pour montrer que f est periodique de periode T=pi tu calcules f(x+pi) et tu montres que c'est egale à f(x)

comme f est periodique de periode T=pi,il suffit d'etudier sur un intervalle de longueur T tq [x1,x1+T] ici x1=-pi/6 don x1+T=5pi/6

1b.pour montrer que I(pi/3,0) est centre de sym il faut que tu te serves de:
I(a,b) est centre de symetrie ssi 2a-x ds Df et si f(2a-x)+f(x)=2b

1c.de même la droite d'equation x=a est axe de symetrie ssi 2a-x ds Df et si f(2a-x)=f(x) dc ici a=2pi/12=pi/6

1d tu resumes tt ce que tu as trouvé ci-dessus f periodique de periode pi,I(pi/3,0) centre de sym. et x=pi/12 axe de sym dc la connaissance de Cf sur [-pi/6,pi/12] permet de connaitre entierement Cf.

2) tu calcules f'(x)=-2sin(2x-pi/6) tu etudies son signe sur [-pi/6,pi/12] tu auras les variation de f

3) a faire par tes soins

partie B :ce n'est pas si complique que ça

A+

[potterboy6274]

Merci pour cette aide, je devrais men sortir, et oui je devais le rendre aujourd'hui mais ma prof est absente don je rend lundi, ce qui me laisse le temps de recommencer le dm .