Exercices sur les coordonnées...
20 messages
- Page 1 sur 1
Exercices sur les coordonnées...
Bonsoir !
comme nous étions en vacances, il n'y avait pas de maths donc je n'ai pas été obligée de venir sur ce forum :P
Mais là, j'ai un problème, je ne suis vraiment pas certaine de quoi il s'agit.
"On donne les points P(-3;2), Q(4;3), R(6;-3) et S(-1;4).
Démontrez que PQRS est un parallèlogramme."
J'aurais utilisé la fomule pour calculer les milieux mais je crois que je suis sur la mauvaise piste en fait... Voilà, si quelqu'un pouvait me faire voir comment on fait pour démontrer..
Merci d'avance.
comme nous étions en vacances, il n'y avait pas de maths donc je n'ai pas été obligée de venir sur ce forum :P
Mais là, j'ai un problème, je ne suis vraiment pas certaine de quoi il s'agit.
"On donne les points P(-3;2), Q(4;3), R(6;-3) et S(-1;4).
Démontrez que PQRS est un parallèlogramme."
J'aurais utilisé la fomule pour calculer les milieux mais je crois que je suis sur la mauvaise piste en fait... Voilà, si quelqu'un pouvait me faire voir comment on fait pour démontrer..
Merci d'avance.
star a écrit:Bonsoir !
comme nous étions en vacances, il n'y avait pas de maths donc je n'ai pas été obligée de venir sur ce forum
Mais là, j'ai un problème, je ne suis vraiment pas certaine de quoi il s'agit.
"On donne les points P(-3;2), Q(4;3), R(6;-3) et S(-1;4).
Démontrez que PQRS est un parallèlogramme."
J'aurais utilisé la fomule pour calculer les milieux mais je crois que je suis sur la mauvaise piste en fait... Voilà, si quelqu'un pouvait me faire voir comment on fait pour démontrer..
Merci d'avance.
Bonjour,
PQRS est un parallèlogramme car : P(-3;2) Q(4;3)=(7;1)
S(-1;4) R(6;-3) =(7;-7)
Il faudrait que PQ(->) = SR(->) pour démontrer que PQSR est un parallélogramme.
Dlzlogic a écrit:Bonjour,
1- Qu'est ce qui caractérise un parallélogramme ?
2- Vous ne pensez pas que le point S n'aurait pas plutôt pour coordonnées(-1;-4) ?
3- avez-vous fait un dessin ?
Bonjour,
Un parallélogramme a ses côtés opposés parallèles.
Ah oui, pardon, j'ai oublié le signe négatif...
Oui, j'ai fait un dessin et ça m'a aidée.
Merci de votre réponse !
Encore désolée mais je suis très mal, j'ai un contrôle de maths vendredi (déjà)....Et je n'ai pas tout compris, loin de là. Par exemple, j'ai un exercice (en tout j'en ai cinq --') à faire, c'est :
"On donne les points (-4;-1), B(4;-2) et C (-2;2). Le triangle ABC est-il rectangle ? "
Je suppose que les coordonnées (-4;-1), c'est le point A mais ce n'était pas marqué.
Je ne sais pas par quels points remplacer les coordonnées. ):
On a fait plusieurs exercices ce matin là-dessus, mais j'en ai eu un seul de bon...
Je pense que la formule c'est racine(Xb -Xa)²+(Yb -Ya)².
Par contre, comme je le disais, je ne sais pas s'il faut remplacer Xa par -4 ou bien 2...Et le reste de même...J'ai relu ma feuille de cours mais je ne comprends pas. Il m'arrive d'avoir bon mais j'ai faux la plupart du temps. Quel est le chiffre à remplacer par Xb ? Par Xa? ....
"On donne les points (-4;-1), B(4;-2) et C (-2;2). Le triangle ABC est-il rectangle ? "
Je suppose que les coordonnées (-4;-1), c'est le point A mais ce n'était pas marqué.
Je ne sais pas par quels points remplacer les coordonnées. ):
On a fait plusieurs exercices ce matin là-dessus, mais j'en ai eu un seul de bon...
Je pense que la formule c'est racine(Xb -Xa)²+(Yb -Ya)².
Par contre, comme je le disais, je ne sais pas s'il faut remplacer Xa par -4 ou bien 2...Et le reste de même...J'ai relu ma feuille de cours mais je ne comprends pas. Il m'arrive d'avoir bon mais j'ai faux la plupart du temps. Quel est le chiffre à remplacer par Xb ? Par Xa? ....
Ok, pas de panique!
Commence par tracer un repère et par placer les points A,B,C.
Ensuite, as-tu entendu parler du théorème de Pythagore au collège? Ce théorème te dit que le triangle ABC est rectangle en en C si et seulement si .
.
Il faut donc savoir calculer AB^2,AC^2 et BC^2 en fonction des coordonnées de A,B,C dans le repère orthonormé que tu considères. Il est très important que ce repère soit orthonormé.
Si x_A est l'abscisse de A, x_B est l'abscisse de B, y_A est lordonnée de A, y_B est lordonnée de B, alors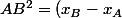^2+(y_B-y_A)^2) .
.
Il est important que tu te rendes compte que cette formule n'est rien d'autre que le théorème de Pythagore dans un triangle ou AB est lhypoténuse, et qui a un coté horizontal et un coté vertical.
Bref, pour vérifier que le triangle ABC est rectangle en C, il faut que tu calcules AB^2, AC^2 et BC^2 et que tu vérifies si légalité est vraie ou fausse.
est vraie ou fausse.
Commence par tracer un repère et par placer les points A,B,C.
Ensuite, as-tu entendu parler du théorème de Pythagore au collège? Ce théorème te dit que le triangle ABC est rectangle en en C si et seulement si
Il faut donc savoir calculer AB^2,AC^2 et BC^2 en fonction des coordonnées de A,B,C dans le repère orthonormé que tu considères. Il est très important que ce repère soit orthonormé.
Si x_A est l'abscisse de A, x_B est l'abscisse de B, y_A est lordonnée de A, y_B est lordonnée de B, alors
Il est important que tu te rendes compte que cette formule n'est rien d'autre que le théorème de Pythagore dans un triangle ou AB est lhypoténuse, et qui a un coté horizontal et un coté vertical.
Bref, pour vérifier que le triangle ABC est rectangle en C, il faut que tu calcules AB^2, AC^2 et BC^2 et que tu vérifies si légalité
Luc a écrit:Ok, pas de panique!
Commence par tracer un repère et par placer les points A,B,C.
Ensuite, as-tu entendu parler du théorème de Pythagore au collège? Ce théorème te dit que le triangle ABC est rectangle en en C si et seulement si.
Il faut donc savoir calculer AB^2,AC^2 et BC^2 en fonction des coordonnées de A,B,C dans le repère orthonormé que tu considères. Il est très important que ce repère soit orthonormé.
Si x_A est l'abscisse de A, x_B est l'abscisse de B, y_A est lordonnée de A, y_B est lordonnée de B, alors.
Il est important que tu te rendes compte que cette formule n'est rien d'autre que le théorème de Pythagore dans un triangle ou AB est lhypoténuse, et qui a un coté horizontal et un coté vertical.
Bref, pour vérifier que le triangle ABC est rectangle en C, il faut que tu calcules AB^2, AC^2 et BC^2 et que tu vérifies si légalitéest vraie ou fausse.
Merci, mais je n'ai pas très bien compris cette phrase: "Si x_A est l'abscisse de A, x_B est l'abscisse de B, y_A est lordonnée de A, y_B est lordonnée de B, alors
Ok. Je te réexplique ce qu'est l'abscisse et lordonnée.
Est-ce que tu sais tracer un repère orthonormé? (c'est deux axes gradués perpendiculaires qui se coupent en un point appelé origine du repère).
Il y a donc un axe horizontal, que l'on appelle l'axe des abscisses.
Il y a aussi un axe vertical que l'on appelle l'axe des ordonnées.
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Par convention, on oriente l'axe des abscisses vers la droite et l'axe des ordonnées vers le haut.
Cela signifie que si l'on se déplace vers la droite, l'abscisse augmente et que si l'on se déplace vers le haut, lordonnée augmente.
Est-ce que tu arrives a placer les points A,B,C sur le repère?
Est-ce que tu sais tracer un repère orthonormé? (c'est deux axes gradués perpendiculaires qui se coupent en un point appelé origine du repère).
Il y a donc un axe horizontal, que l'on appelle l'axe des abscisses.
Il y a aussi un axe vertical que l'on appelle l'axe des ordonnées.
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Par convention, on oriente l'axe des abscisses vers la droite et l'axe des ordonnées vers le haut.
Cela signifie que si l'on se déplace vers la droite, l'abscisse augmente et que si l'on se déplace vers le haut, lordonnée augmente.
Est-ce que tu arrives a placer les points A,B,C sur le repère?
Luc a écrit:Ok. Je te réexplique ce qu'est l'abscisse et lordonnée.
Est-ce que tu sais tracer un repère orthonormé? (c'est deux axes gradués perpendiculaires qui se coupent en un point appelé origine du repère).
Il y a donc un axe horizontal, que l'on appelle l'axe des abscisses.
Il y a aussi un axe vertical que l'on appelle l'axe des ordonnées.
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Par convention, on oriente l'axe des abscisses vers la droite et l'axe des ordonnées vers le haut.
Cela signifie que si l'on se déplace vers la droite, l'abscisse augmente et que si l'on se déplace vers le haut, lordonnée augmente.
Est-ce que tu arrives a placer les points A,B,C sur le repère?
Oui, je sais ce qu'est un repère orthonormé et j'ai placé les points. Pour moi, juste comme ça, le triangle est rectangle mais par le calcul, ça ne me donne pas même résultat....Je ne sais pas dans quel ordre mettre les chiffres, c'est grave..
Je vais donc te répéter ce que j'ai dit, c'est suffisant pour savoir dans quel ordre mettre les chiffres.
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Le point A (x_A,y_A) est le point d'abscisse x_A et dordonnée y_A
Application a ton exercice :
A(-4;-1), B(4;-2) et C (-2;2).
Question : Que valent l'abscisse de A, lordonnée de A, l'abscisse de B, lordonnée de B, l'abscisse de C, lordonnée de C?
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Le point A (x_A,y_A) est le point d'abscisse x_A et dordonnée y_A
Application a ton exercice :
A(-4;-1), B(4;-2) et C (-2;2).
Question : Que valent l'abscisse de A, lordonnée de A, l'abscisse de B, lordonnée de B, l'abscisse de C, lordonnée de C?
Luc a écrit:Je vais donc te répéter ce que j'ai dit, c'est suffisant pour savoir dans quel ordre mettre les chiffres.
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Le point A (x_A,y_A) est le point d'abscisse x_A et dordonnée y_A
Application a ton exercice :
A(-4;-1), B(4;-2) et C (-2;2).
Question : Que valent l'abscisse de A, lordonnée de A, l'abscisse de B, lordonnée de B, l'abscisse de C, lordonnée de C?
L'abscisse de A = - 4 , l'ordonnée de A= - 1, l'abscisse de B = 4, l'ordonnée de B= -2, l'abscisse de C= -2 et l'ordonnée de C = 2.
Luc a écrit:Je vais donc te répéter ce que j'ai dit, c'est suffisant pour savoir dans quel ordre mettre les chiffres.
Un point peut être représenté par deux nombres : son abscisse et son ordonnée.
Par convention, le point (x,y) est le point dabscisse x et dordonnée y.
Par exemple, le point (2,4) est le point d'abscisse 2 et dordonnée 4.
Le point A (x_A,y_A) est le point d'abscisse x_A et dordonnée y_A
Application a ton exercice :
A(-4;-1), B(4;-2) et C (-2;2).
Question : Que valent l'abscisse de A, lordonnée de A, l'abscisse de B, lordonnée de B, l'abscisse de C, lordonnée de C?
2,4 c'est 2;4 non ??
Je dirais que l'abscisse de A vaut x_A , l'ordonnée de A vaut y_A, l'abscisse de B vaut x_B, son ordonnée y_B, l'abscisse de C vaut x_c et enfin son ordonnée vaut y_C.
star a écrit:2,4 c'est 2;4 non ??
Oui.
star a écrit:Je dirais que l'abscisse de A vaut x_A , l'ordonnée de A vaut y_A, l'abscisse de B vaut x_B, son ordonnée y_B, l'abscisse de C vaut x_c et enfin son ordonnée vaut y_C.
Oui, en général, mais que valent ces nombres pour les points de l'exercice, sachant qu'on a écrit A(-4;-1), B(4;-2) et C (-2;2) ?
Luc a écrit:Oui c'est exactement ça!
Du coup, calculonspar exemple.
Quels sont les nombres que tu mets dans la formule?
En d'autres termes, que vaut?
Bon, déjà c'est ça.
Heulàà ! C'est que j'ai toujours besoin de la formule sinon j'ai du mal...
Mais en fait, les chiffres (4-(-4))² + (-2-(-1))² sont ceux qu'il faut placer dans la formule ?
star a écrit:Bon, déjà c'est ça.
Qu'est-ce qui est quoi? J'ai du mal a suivre :we:
star a écrit:Heulàà ! C'est que j'ai toujours besoin de la formule sinon j'ai du mal...
C'est normal.
star a écrit:Mais en fait, les chiffres (4-(-4))² + (-2-(-1))² sont ceux qu'il faut placer dans la formule ?
Ce ne sont pas des chiffres mais des nombres.
Et effectivement,
Combien vaut
Luc a écrit:Qu'est-ce qui est quoi? J'ai du mal a suivre :we:
C'est normal.
Ce ne sont pas des chiffres mais des nombres.
Et effectivement,. C'est l'application de la formule
pour les points particuliers A(4;-2) et B(-4;-1).
Combien vaut? (c'est uniquement du calcul)
J'ai juste répondu à ton affirmation "oui, c'est exactement ça !" ^^
Le résultat c'est 65.
20 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
