Exercice de logique et d'ensembles

[Jibrilarto]

Bonjour, j'ai un exercice avec les données suivantes:
pour a et b deux réels distincts: E= x∈ R/ x²+2bx+a=0 F=x∈ R/ x²+2ax+b=0
la première question est de montrer x∈ E∩F ⇒ x=1/2 , ce qui est facile
la deuxième question est de montrer que : E∩F=/=∅ ⇒ a+b= -1/4 , la je me suis bloquée, car dans le cas ou E∩F, x=1/2, x²+2bx+a=x²+2ax+b, l'expression devient a+b=a+b, alors a,b ∈ R, je ne sais pas quoi faire, merci en avance

[lyceen95]

Si est non-vide, 1/2 est solution de nos 2 équations. Ok.
Donc si est non-vide, on peut remplacer x par 1/2 dans , et dire que ce résultat vaut 0.
Et du coup ...

[capitaine nuggets]

Salut !

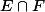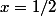La première question signifie que . Donc si l'on suppose l'intersection non vide alors nécessairement . Or que se passe-t-il si ? Eh bien, les réels a et b vérifient les conditions et , c'est-à-dire ...

[Jibrilarto]

Merci beacoup