Exercice de demonstration de symétrie axiale entre deux courdes-terminale s

[marmorata]

Bonjour à tous !
Je suis en train de faire un dm portant principalement sur une étude de fonctions et je bloque pour la dernière question. Elle demande d'abord de tracer les courbes Cf et Cf2 representatives des fonctions f(x)=x+racinede(x^2-1) et f2(x)=x-racinede(x^2-1)
J'ai tracé ces deux courbes puis l'énoncé demande que constate-t-on ?
Je constate que ces deux courbes sont symétriques par raport à l'origine du repère soit le point O(0;0)
L'énoncé demande enfin de demontrer cette constatation et c'est là que je bloque, je ne voit pas du tout comment demontrer cela.
Merci de votre Aide !!!

[zygomatique]

salut

calcule f1(x) + f2(-x) ...

[chan79]

tu pourrais aussi tracer la droite de pente 2 qui passe par l'origine et conjecturer puis démontrer autre chose
La réunion des deux courbes forme une hyperbole

[marmorata]

J'ai caluculé f1(x)+f2(x) et ça donne 2x mais je ne comprend pas vraiment à quoi cela correspond et pour l'hyperbole je suis d'accord que la réunion des deux courbes en forme une mais comment le demontrer ? Merci beaucoup de m'aider ;)

[chan79]

'

J'ai caluculé f1(x)+f2(x) et ça donne 2x mais je ne comprend pas vraiment à quoi cela correspond et pour l'hyperbole je suis d'accord que la réunion des deux courbes en forme une mais comment le demontrer ? Merci beaucoup de m'aider

zygomatique t'a proposé de calculer f1(x)+f2(-x)
En faisant un bon changement de repère, l'équation de la réunion des courbes est



avec (nombre d'or, encore lui...)

et

C'est l'équation d'une hyperbole, avec ses deux axes de symétrie et son centre de symétrie.

Je crains que ce ne soit pas de niveau lycée ?

[siger]

Bonjour

zygomatique parle de f2(-x)....

on a affaire a une symetrie centrale et non axiale:
un point M(x0,y0) du plan a pour symetrique par rapport a l'origine le point N(-x0,-y0)

soit un point P(x0,y0) sur f1 tel que f1(x0) = x0+V(x0²-1) = y0
le point P'(-x0,-y0) sur f2 tel que f2(-x0) = -x0-V(x0²-1) = -y0 est donc le symetrique de P

[zygomatique]

f1(x) + f2(-x) = 0

si M(x, f1(x)) est un point de Cf1 alors N(-x, f2(-x)) est un point de Cf2 ... et réciproquement donc l'union des deux courbes est symétriques par rapport à l'origine (puisque M et N le sont)

...

[chan79]

'


C'est l'équation d'une hyperbole, avec ses deux axes de symétrie et son centre de symétrie.

Je crains que ce ne soit pas de niveau lycée ?

il y a peut-être un moyen de niveau lycée
un point (x,y) appartient à l'union des deux courbes si:


soit






en permutant et :




et il ne reste plus qu'à montrer que la représentation graphique de cette fonction admet deux axes de symétrie

[marmorata]

J'ai maintenant bien compris comment démontrer que les deux courbes sont symétriques par rapport au centre du repère et je vous remercie beaucoup ! En ce qui concerne l'hyperbole je vois très bien ce qui est à demontrer mais je ne comprend pas trop la demonstration que vous m'avez proposée ..

[chan79]

J'ai maintenant bien compris comment démontrer que les deux courbes sont symétriques par rapport au centre du repère et je vous remercie beaucoup ! En ce qui concerne l'hyperbole je vois très bien ce qui est à demontrer mais je ne comprend pas trop la demonstration que vous m'avez proposée ..

Tu peux suivre les étapes suivantes mais c'est un peu long.
1°) Montrer que la droite d'équation est une asymptote de f1. Pour cela, montre que tend vers quand x tend
vers +
2°) Tracer la bissectrice de l'angle formé par cette droite et l'axe des x. (en pointillés rouges ci-dessus)
3°) Montrer que la tangente de l'angle vert est égale à 2.
4°) En déduire que la tangente de l'angle rouge est
(utiliser tan(2a)=2tan(a)/(1-tan²(a))
5°) Montrer qu'une équation de la bissectrice est
6°) Montrer que si un point M du plan a comme coordonnées , son symétrique M' par rapport à la bissectrice a comme coordonnées et :




Utiliser une condition d'orthogonalité et une condition de colinéarité.

7°)Montrer que appartient à l'union des deux courbes si
c'est fait précédemment
8°) Montrer que si les coordonnées x et y de M vérifient , alors
Conclure

[zygomatique]

quasi impossible pour un terminale de maintenant ..... :cry:



1/ tracer les courbes des fonctions f et g pour voir ... (et avec les logiciels de maintenant c'est easy)

2/ constater que 0 est centre de symétrie de l'union des deux courbes

3/ savoir traduire algébriquement qu'un point (ici l'origine O ce qui est encore plus simple) est centre de symétrie d'une courbe

4/ calculer f(x) + g(-x) et conclure ...


mais ce cheminement intellectuel est tout aussi inexistant chez un terminale de maintenant .... :cry:

[chan79]

quasi impossible pour un terminale de maintenant .....

:

Il y en a encore des bons, j'en suis sûr.
Ici, il est question de symétrie axiale dans le titre. Je ne sais pas si on peut faire plus simple.

[zygomatique]

effectivement si on veut montrer la symétrie axiale alors je suis d'accord avec ton cheminement ....

[Ben314]

Je sais pas si j'aurais fait comme ça si je devais faire un exo de terminale concernant la symétrie en question.
J'aurais sans doute plutôt demandé de déterminer, en fonction de a et b le nombre de points d'intersection de la courbe C d'équation et de la droite D d'équation y=ax+b.
On trouve deux pentes a "particulières" (0 et 2) qui sont les pentes des deux asymptotes où il y a un seul point d'intersection sauf pour une valeur particulière de b (0 dans les deux cas) où l'intersection est vide et qui correspond aux asymptotes elle même.
Ensuite, j'aurais demandé de montrer que, pour a fixé distinct de 0 et 2 et b variable, lorsqu'il y a deux points d'intersection, le milieu du bipoint décrit une portion d'une droite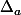 dont on déterminera une équation.
Enfin j'aurais terminé en demandant pour quelles valeurs de la droite 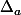est-elle perpendiculaire aux droites d'équations et d'interpréter le résultat (-> deux axes de symétrie orthogonale)

L'intérêt de la méthode :
1) Éviter de manipuler des angles et en particulier des bissectrices
2) On peut appliquer la même méthode a absolument n'importe quelle conique et en déduire ces axes de symétrie.