Exercice 1èreS barycentre

par **daam-iien** » 28 Oct 2010, 10:59

Bonjour, je suis en 1èreS et je bloque totalement sur un exercice de mon DM sur les barycentre :

" Exercice 2 : Coefficient barycentrique définis par un paramètre
A, B et C sont trois points données du plan et m est un nombre réel.
A quel condition sur m, le barycentre Gm des points pondérés ( A,7m²), (b,m² + m), (C,-3-m) existe-t-il ? Justifier "

Si quelqu'un pourrait m'expliquer ou m'orienter je le remercie d'avance

par **Jimm15** » 28 Oct 2010, 11:04

Coucou,

Le barycentre de points pondérés existe si, et seulement si, la somme de leurs coefficients est non nulle !!

par **daam-iien** » 28 Oct 2010, 11:09

Donc enfaite sa serait lorsque 7m² + m² + m - 3 - 3m soit 8m² - 2m - 3 différent de zero ? et j'en ai fini la ? Sa serait aussi simple que sa ? :P

par **Jimm15** » 28 Oct 2010, 11:14

daam-iien a écrit:Donc enfaite sa serait lorsque 7m² + m² + m - 3 - 3m soit 8m² - 2m - 3 différent de zero ? et j'en ai fini la ? Sa serait aussi simple que sa ?

Cest un bon début.
Maintenant, il faut peut-être déterminer les valeurs de

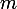
pour lesquelles cette inégalité est vérifiée. :lol5:

par **daam-iien** » 28 Oct 2010, 11:17

Ok merci mais on sèche toujours --' ( on est 2 la dessus :) ), quelques piste pour savoir vers quoi on doit aller ? :P

par **Jimm15** » 28 Oct 2010, 11:21

daam-iien a écrit:Ok merci mais on sèche toujours --' ( on est 2 la dessus ), quelques piste pour savoir vers quoi on doit aller

Calculer le discriminant du trinôme du second degré

(en fonction de

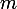
) puis choisir les valeurs de

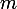
pour lesquelles ...

par **daam-iien** » 28 Oct 2010, 11:28

J'obtient discriminant = 100
M1 = 3/4
M2 = -1/2

Mais je sèche de nouveaux --' en effet on faisait des inéquation du style 8m² - 2m - 3 < ou > 0 mais la ce n'est pas le cas ...

par **Jimm15** » 28 Oct 2010, 11:31

daam-iien a écrit:J'obtient discriminant = 100
M1 = 3/4
M2 = -1/2

Mais je sèche de nouveaux --' en effet on faisait des inéquation du style 8m² - 2m - 3 0 mais la ce n'est pas le cas ...

Il y a donc 2 valeurs de

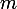
pour lesquelles le trinôme sannule. Quelles sont les valeurs de

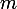
pour lesquelles il ne sannule pas ?

par **daam-iien** » 28 Oct 2010, 11:36

Ainsi S = ]infini ; -1/2[U]-1/2 ; 3/4[U]3/4 ; + infini[
Je sais pas si on peut écrire ceci comme sa ?

par **Jimm15** » 28 Oct 2010, 11:41

daam-iien a écrit:Ainsi S = ]infini ; -1/2[U]-1/2 ; 3/4[U]3/4 ; + infini[
Je sais pas si on peut écrire ceci comme sa ?

Si, cest correct.
Pour faire moins « lourd », tu peux écrire simplement :

.

par **daam-iien** » 28 Oct 2010, 11:44

D'accord merci beaucoup a toi :) passe une bonne journée

par **Jimm15** » 28 Oct 2010, 11:45

Toi aussi.

Exercice 1èreS barycentre

Exercice 1èreS barycentre

Qui est en ligne