Bonjour.
J'ai a faire, por le mois de septembre, une étude complète de la fonction X³/(X²-1). Suite à des essais infructueux, j'ai fait tracer le graphique par ma calculatrice, et je devine une asymptote horizontale a gauche en -3 et à droite en +3, 2 asymptotes verticales en + 1 et -1. On voit également très clairement que le signe de la dérivée devrait être toujours négatif, vu que la courbe ne fait que descendre, et qu'il doit y avoir un point d'inflexion en (0;0).
Seulement, par les méthodes de calcul apprises en classe, je ne trouve pas du tout cela. J'arrive au résultat suivant qui ne semble pas correspondre au graphique: (X^4-3X²)/[(x²-1)²] (désolé, je ne sais pas comment écrire les exposant au dessus de ³ sur mon clavier).
D'après cette dérivée, je trouve les racines 0 et +/-V3 (je ne sais pas non plus écrire les racines :hum: ) , je déduis que le signe de la dérivée est positif avant -V3, négatif ensuite, puis négatif entre 0 et V3 et finalement positif.
La dérivée seconde semble anormalement compliquée et longue, avec un facteur en X^7 :mur: , or nous ne savons pas comment chercher les 0 des fonction supérieures au deuxième degré.
J'en suis la. je ne comprend pas comment je peux trouver une dérivée contenant un ou plusieurs facteurs en X si elle doit être toujours négative.
Ai-je manqué quelque chose? une factorisation peut être, ou ai-je fait une erreur dans ma dérivée première? Ce qui mennuie, c'est que mon prof m'a dit que la fonction était "on ne peut plus simple."
Merci d'avoir lu le pavé pas très digeste. :happy2:
Etude graphique de fonction X³/(X²-1)
12 messages
- Page 1 sur 1
salut
(x^2 + x + 1) + 1)
donc = \dfrac {x^3}{x^2 - 1} = x + \dfrac {1}{x + 1} + \dfrac {1}{x^2 - 1} = x + \dfrac 1 2 \left (\dfrac {1}{x + 1} + \dfrac {1}{x - 1} \right))
donc deux asymptotes verticales d'équation x = 1 et x = -1 et une asymptote oblique d'équation y = x
d'autre part le numérateur de f'(x) est(x + \sqrt 3))
évidemment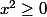 donc n'intervient pas pour le signe mais fait apparaître une tangente horizontale en l'origine (car f(0) = 0)
donc n'intervient pas pour le signe mais fait apparaître une tangente horizontale en l'origine (car f(0) = 0)
d'autre part le trinome est positif à l'extérieur des racines ...
tu as donc tout pour établir les variations de f
....
et le point d'inflexion est donc l'origine ...
donc
donc deux asymptotes verticales d'équation x = 1 et x = -1 et une asymptote oblique d'équation y = x
d'autre part le numérateur de f'(x) est
évidemment
d'autre part le trinome est positif à l'extérieur des racines ...
tu as donc tout pour établir les variations de f
....
et le point d'inflexion est donc l'origine ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Salut !
Soit la fonction définie par
la fonction définie par =\frac{x^3}{x^2-1}) et on note
et on note  sa courbe représentative dans un repère orthonormé direct
sa courbe représentative dans un repère orthonormé direct ) .
.
1°) Détermine le domaine de définition de la fonction
de la fonction  .
.
2°) Montre que est impaire i.e.
est impaire i.e. = -f(x)) . Qu'en déduis-tu pour la courbe représentative
. Qu'en déduis-tu pour la courbe représentative  de
de  ?
?
3°) D'après l'argument précédent, on est seulement ramené à étudier sur
sur  (comprends-tu pourquoi ?).
(comprends-tu pourquoi ?).
4°) Étudie donc les limites aux bornes du domaine .
.
5°) Exprime la dérivée de
de  puis étudie son signe sur
puis étudie son signe sur  .
.
6°) Enfin, en effectuant la division euclidienne de par
par 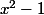 , montre que
, montre que  admet une asymptote oblique
admet une asymptote oblique  d'équation
d'équation 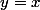 .
.
:+++:
Soit
1°) Détermine le domaine de définition
2°) Montre que
3°) D'après l'argument précédent, on est seulement ramené à étudier
4°) Étudie donc les limites aux bornes du domaine
5°) Exprime la dérivée
6°) Enfin, en effectuant la division euclidienne de
:+++:
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonjour Kuriboh0 ! Le tracé de la calculatrice, tel que tu le décris, ne semble pas correspondre à la fonction. Par exemple tu dis qu'elle est décroissante, alors qu'elle tend vers plus l'infini en plus l'infini.
Ça, c'est l'expression de la dérivée. OK, j'ai trouvé pareil.
Moi aussi.
Après calcul rapide (à vérifier), je trouve :
 = \frac{2x^5+4x^3-6x}{(x^2-1)^4})
Il me semble bien que les termes en x^7 s'annulent.
Ensuite, pour résoudre f"(x)=0, il suffit de factoriser :
 = 0 \Leftrightarrow x=0 \mbox{ ou } x^4+2x^2-3=0)
L'équation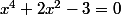 se résout en posant X=x².
se résout en posant X=x².
J'arrive au résultat suivant qui ne semble pas correspondre au graphique: (X^4-3X²)/[(x²-1)²]
Ça, c'est l'expression de la dérivée. OK, j'ai trouvé pareil.
je déduis que le signe de la dérivée est positif avant -V3, négatif ensuite, puis négatif entre 0 et V3 et finalement positif.
Moi aussi.
La dérivée seconde semble anormalement compliquée et longue, avec un facteur en X^7 , or nous ne savons pas comment chercher les 0 des fonction supérieures au deuxième degré.
Après calcul rapide (à vérifier), je trouve :
Il me semble bien que les termes en x^7 s'annulent.
Ensuite, pour résoudre f"(x)=0, il suffit de factoriser :
L'équation
L'astuce d'@zygomatique avec la factorisation du numérateur de la dérivée est la bonne (je pense) , la dérivée va s'annuler en - racine 3 , 0 et racine de 3 . Df est ]-infini ,-1[U ]1,+infini[ puisque le dénominateur peut s'annuler en 1 et -1 (donc ces valeurs ne sont pas inclues , le dénominateur ne doit jamais s'annuler) .
Sinon ,pour prouver l'existence d'une asymptote oblique y=x, tu dois faire limite à l'infini de [f(x) - x] et obtenir 0 , et comme par exemple 1/x tend vers 0 à l'infini , tu peux déduire facilement avec la simplification faite par @zygomatique .
Sinon ,pour prouver l'existence d'une asymptote oblique y=x, tu dois faire limite à l'infini de [f(x) - x] et obtenir 0 , et comme par exemple 1/x tend vers 0 à l'infini , tu peux déduire facilement avec la simplification faite par @zygomatique .
lulubibi28 a écrit:L'astuce d'@zygomatique avec la factorisation du numérateur de la dérivée est la bonne (je pense) , la dérivée va s'annuler en - racine 3 , 0 et racine de 3 . Df est ]-infini ,-1[U ]1,+infini[ puisque le dénominateur peut s'annuler en 1 et -1 (donc ces valeurs ne sont pas inclues , le dénominateur ne doit jamais s'annuler) .
Sinon ,pour prouver l'existence d'une asymptote oblique y=x, tu dois faire limite à l'infini de [f(x) - x] et obtenir 0 , et comme par exemple 1/x tend vers 0 à l'infini , tu peux déduire facilement avec la simplification faite par @zygomatique .
non l'ensemble de définition de f est
il est symétrique par rapport à 0 et f(-x) = -f(x) donc effectivement f est impaire ...
0 est racine double de la dérivée donc racine simple de la dérivée seconde dont point d'inflexion .... mais ça ne dit pas qu'il n'y en ait pas d'autre ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
C'est plutôt facile de démonter que la fonction est impaire ...
Un point d'inflexion correspond au point où la courbe change brusquement de forme , mais l'ensemble de définition I serait donc ]- infini, -1[ U ]-1, 1[ U [0, +infini[ ,non ? (mais c'est pas possible 0 est inférieur à 1 donc y'a plus le ]-1, 1[ en principe)
Il faudrait aussi étudier la position de l'asymptote oblique par rapport à la fonction
et donc calculer les limites de la fonction f sur les bornes de I.Le point d'inflexion (0,0)est déterminée par la dérivée seconde , mais la fonction f est bien croissante , puis décroissante , croissante , puis décroissante vers l'infini .
Un point d'inflexion correspond au point où la courbe change brusquement de forme , mais l'ensemble de définition I serait donc ]- infini, -1[ U ]-1, 1[ U [0, +infini[ ,non ? (mais c'est pas possible 0 est inférieur à 1 donc y'a plus le ]-1, 1[ en principe)
Il faudrait aussi étudier la position de l'asymptote oblique par rapport à la fonction
et donc calculer les limites de la fonction f sur les bornes de I.Le point d'inflexion (0,0)est déterminée par la dérivée seconde , mais la fonction f est bien croissante , puis décroissante , croissante , puis décroissante vers l'infini .
mon expression de f donne immédiatement la position de la courbe de f par rapport à son asymptote oblique ....
l'étude du signe de f' donne immédiatement que f est décroissante sur l'intervalle ]-1, 1[ ...
ensuite f est évidemment croissante au voisinage des infinis ... puisqu'elle se comporte comme son asymptote oblique ....
l'étude du signe de f' donne immédiatement que f est décroissante sur l'intervalle ]-1, 1[ ...
ensuite f est évidemment croissante au voisinage des infinis ... puisqu'elle se comporte comme son asymptote oblique ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Ok . Cet exercice est un peu tordu ^^ , et typiquement filière S . En tout cas , je compatis avec ceux qui ont pu avoir ce genre d'exo au bac ...
Et l'ensemble de définition de I ? L'intervalle ]-1, 1[ disparait en principe ... (d'ailleurs , pourquoi inclure cette intervalle dans Df , puisque ces valeurs sont déjà interdites )
lulubibi28 a écrit:C'est plutôt facile de démonter que la fonction est impaire ...
Un point d'inflexion correspond au point où la courbe change brusquement de forme , mais l'ensemble de définition I serait donc ]- infini, -1[ U ]-1, 1[ U [0, +infini[ ,non ? (mais c'est pas possible 0 est inférieur à 1 donc y'a plus le ]-1, 1[ en principe)
Il faudrait aussi étudier la position de l'asymptote oblique par rapport à la fonction
et donc calculer les limites de la fonction f sur les bornes de I.Le point d'inflexion (0,0)est déterminée par la dérivée seconde , mais la fonction f est bien croissante , puis décroissante , croissante , puis décroissante vers l'infini .
Et l'ensemble de définition de I ? L'intervalle ]-1, 1[ disparait en principe ... (d'ailleurs , pourquoi inclure cette intervalle dans Df , puisque ces valeurs sont déjà interdites )
lulubibi28 a écrit:Ok . Cet exercice est un peu tordu ^^ , et typiquement filière S . En tout cas , je compatis avec ceux qui ont pu avoir ce genre d'exo au bac ...
Et l'ensemble de définition de I ? L'intervalle ]-1, 1[ disparait en principe ... (d'ailleurs , pourquoi inclure cette intervalle dans Df , puisque ces valeurs sont déjà interdites )
pourquoi tu ne peux pas calculer f(0) ? f(-1/2) ? f(pi/4) ? ...
que doit-on vérifier quand on a un quotient ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
On peut calculer aisément les valeurs de x que tu as proposé .
Mais lorsqu'on a un quotient , il faut vérifier que le dénominateur ne s'annule pas , par contre le numérateur peut s'annuler (y'a pas de soucis) .
J'ai posé une question dans mon post précèdent sur l'intervalle I :hein: ( le 0 est entre le -1 et le 1 )
Mais lorsqu'on a un quotient , il faut vérifier que le dénominateur ne s'annule pas , par contre le numérateur peut s'annuler (y'a pas de soucis) .
J'ai posé une question dans mon post précèdent sur l'intervalle I :hein: ( le 0 est entre le -1 et le 1 )
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
