A la demande de Benekire2, je poste un exercice sur le 3e degré intéressant selon moi, mais si vous voulez le faire ou poser des questions, vous êtes les bienvenus ^^ , voilà :++:.
Le but de cet exercice est de trouver le nombre de solutions de l'équation

selon les valeurs de

,

,

et

.
A. Cas de l'équation 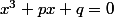

est la fonction définie sur

par
=x^3+px+q)
où

et

sont deux réels donnés.
1. Etudier les variations de

et dresser son tableau de variations. (On distinguera deux cas :

et

, l'équation
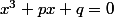
admet exactement une solution et une seule. Illustrer le schéma par une figure.
d) Démontrer que si le produit

, l'équation
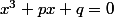
admet exactement trois solutions.
4. En déduire le nombre de solutions des équations suivantes et controler éventuellement votre résultat à la calculatrice.
a)

;
b)

;
c)

;
d)

.
B. Cas de l'équation 

où b,c et d sont trois réels donnés.
1. Démontrer qu'en posant

, l'équation

se ramène à

et

. (On déterminera

et

en fonction de

,

et

).
2. En déduire pour chacunes des équations suivantes :
- Le nombre de solutions.
- A l'aide de la calculatrice, un encadrement d'amplitude
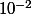
de chacunes des solutions.
a)

;
b)

;
c)

.
