Bonjour, à la demande de Benekire2, je vous propose un exercice un peu long bien qu'assez guidé, amusez-vous bien :++: .
)
est un repère orthonormal. A tout point

de coordonnées
)
, on associe l'équation du second degré d'inconnue

,

)
.
1°)a) Démontrer que "

" équivaut à "l'équation que
)
a deux racines".
b) Tracer, dans le repère
)
, la parabole

d'équation

, puis représentez graphiquement l'ensemble des points
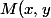)
pour lesquels
)
a deux racines distinctes, puis ceux pour lesquels
)
a une racine double, enfin ceux pour lesquels
)
n'a pas de racines.
2°)

est un point de

d'abscisse

. Prouver que la tangente à

en

a pour équation

.
3°)
Question intermédiaireOn se propose de trouver à quelle condition nécessaire et suffisante, une droite

d'équation

, avec
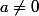
, est tangente à

.
a) Prouver que si

est tangente à

au point
)
, alors
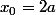
et

.
b) Réciproquement, prouver que la droite

d'équation

,
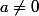
, est tangente à

au point de coordonnée
)
. En conclusion, dire que "la doite

d'équation

est tangente à

" équivaut à dire que

. Et dans ce cas, le point de contact a pour coordonnées
)
.
4°) On considère les équations :
)
:

et
)
:

.
a) Vérifier que
)
et
)
ont une racine commune.
b) Placer sur la figure les points
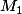
et
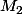
associés à
)
et
)
, et demontrer que la droite
)
est tangente à

.
5°) D'une manière plus générale, on considère les équatiuons :
)
:

et
)
:

, et on suppose que ces équations ont une racine commune

. On note toujours
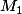
et
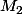
les points associés à ces équations. On suppose

.
a) Exprimer
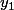
en fonction de

et

, et
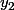
en fonction de

et

.
b) En déduire que
)
a pour équation

et qu'elle est tangente à la parabole

. Préciser les coordonnées du point de contact.
6°) Réciproquement, on suppose que les points distincts
)
et
)
sont tels que la droite
)
est tangente à

.
Les équations
)
et
)
ont-elles au moins une racine commune ?
Est-il possible que
)
et
)
aient deux racines communes lorsque

ou

?
