Etude de fonction ( Tale ES )

[ptitlou]

Bonjour !
J'aurais besoin d'aide pour un exercice sur une étude de fonction :
f(x) = (2.5+x)e^(-0.5x+1)

1) Etudier le sens de variation de f

je sais qu'il faut dériver mais je n'y suis pas arrivé

2) Calculer lim f(x) en -~

3) Vérifier que pour tout réel x : f(x) = 2.5/ e^(0.5x-1) + 2e * 0.5x/e^(0.5x)
En déduire lim f(x) en +~

[annick]

Bonjour

Ta fonction est f(x) = (2.5+x)e^(-0.5x+1), c'est-à-dire qu'elle est de la forme u.v avec u=(2.5+x) et v=e^(-0.5x+1)

Quelle est la dérivée de u.v ? (formule de ton cours)

Quelle est la dérivée u' de u=(2.5+x)
Quelle est la dérivée v' de v=e^(-0.5x+1) (sachant que (e^u)=u'(e^u)

[ptitlou]

je l'ai calculer déjà mais j'arrive pas a un resultat correct j'ai du me tromper quelque part !

sa donne :
u(x) = 2.5 +x et u'(x) = 1
v(x) = e^-0.5x+1 et v'(x) = -0.5

La formule est : (uv)' = u'v+uv'

[Ericovitchi]

la dérivée d'un produit uv c'est u'v+v'u
et la dérivée d'un fonction c'est
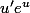
Avec ça tu devrais y arriver.

les limites ne sont pas bien difficile à trouver.

(attention v' ça n'est pas ça)

[ptitlou]

c'est donc pour sa que je me suis trompé v'(x) reste donc -0.5x+1 !???

[Ericovitchi]

non je t'ai dit que la dérivée d'un e^u c'était u'.e^u
tu n'as pas écris ça.

[ptitlou]

oui pardon !
sa fait -0.5e^-0.5x+1

[ptitlou]

c'est ça !???

[Ericovitchi]

oui oui mais donnes la dérivée en entier, on ne va pas faire un post chaque fois que tu additionnes deux machins. Dis nous juste si tu arrives à étudier le sens de variation de la fonction.