étude fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
laureen
- Messages: 6
- Enregistré le: 05 Déc 2012, 13:08
-
 par laureen » 05 Déc 2012, 13:21
par laureen » 05 Déc 2012, 13:21
Bonjour, j'aurai besoin d'aide pour mon devoir maison que je dois rendre demain :$ ..
voici l'énoncé:
f est la fonction définie sur R par f(t) = e^-t2 ( au carré) / 10^^4
c est sa courbe dans un repère orthogonal
1. on désigne par f' la fonction dérivée de f.
a) calculer l'expression de f'(t) pour tout réel t.
b)en déduire le tableau de variation f sur R
Quel est le maximum de cette fonction?
c) Tracer avec la calculatrice la courbe représentative de f. Résoudre graphiquement pui s par le calcul l'équation f(t)=e^-4
2. on admet que la probabilité qu'un certain type de "catastrophe naturelle" ne se produise pas pendant les t années à venir est donnée par f(t)=e-t2 ( au carré) / 10^4 ou t désigne un nombre réel positif
a) calculer f(10) à 10^-2 près et interpréter concrétement le résultat
b) calculer la probabilité que cette catastrophe ne se produise pas pendant les 50 ans a venir. arrondir a 10^-2.
c) calculer la probabilité que cette catastrophe se produise dans les 20 porchaines années
d) une compagnie d'assurance estime que le niveau des cotisations de ses clients est satisfaisant tant que le risque de ce type de catastrophe reste inférrieur a 50%. Utiliser l'affichage du logicile Xcas et une argumentation précise pour indiquer pendant combien d'années cette couverture des risques restera rentable.
En espérant que vous allez m'aider
-
homeya
- Membre Relatif
- Messages: 218
- Enregistré le: 05 Mar 2012, 10:20
-
 par homeya » 05 Déc 2012, 13:31
par homeya » 05 Déc 2012, 13:31
Bonjour,
La fonction est-elle bien f(t) =

?
Cordialement.
-
laureen
- Messages: 6
- Enregistré le: 05 Déc 2012, 13:08
-
 par laureen » 05 Déc 2012, 13:33
par laureen » 05 Déc 2012, 13:33
homeya a écrit:Bonjour,
La fonction est-elle bien f(t) =

?
Cordialement.
Euh non escusé moi c'est pas celle-ci: c'est e - t2/10^4 , le e est exclu de la division
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 05 Déc 2012, 13:37
par Sylviel » 05 Déc 2012, 13:37
"e - t2/10^4" ce n'est pas clair du tout. Donc soit tu écris en latex (il y a un post qui explique comment) soit tu mets des parenthèses pour que l'on sache de quoi tu parles... La proposition de homeya était effectivement la plus naturelle.
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
laureen
- Messages: 6
- Enregistré le: 05 Déc 2012, 13:08
-
 par laureen » 05 Déc 2012, 13:45
par laureen » 05 Déc 2012, 13:45
e ((-t²)/(10^4))
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 05 Déc 2012, 14:31
par Sylviel » 05 Déc 2012, 14:31
ok. Donc as-tu réussi à calculer la dérivée ?
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
laureen
- Messages: 6
- Enregistré le: 05 Déc 2012, 13:08
-
 par laureen » 05 Déc 2012, 14:33
par laureen » 05 Déc 2012, 14:33
Sylviel a écrit:ok. Donc as-tu réussi à calculer la dérivée ?
J'ai pris la formule (u/v)' mais aprés je n'arrive pas a dérivé ..
-
homeya
- Membre Relatif
- Messages: 218
- Enregistré le: 05 Mar 2012, 10:20
-
 par homeya » 05 Déc 2012, 15:13
par homeya » 05 Déc 2012, 15:13
Il faut utiliser avant tout (
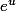
)' = u'
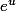
.
-
laureen
- Messages: 6
- Enregistré le: 05 Déc 2012, 13:08
-
 par laureen » 05 Déc 2012, 15:23
par laureen » 05 Déc 2012, 15:23
homeya a écrit:Il faut utiliser avant tout (
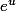
)' = u'
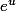
.
D'accord merci beaucoup
Donc pour u je prend e-t² ainsi que pour u'
et pour v je prend 10^4 et v' aussi ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 05 Déc 2012, 17:54
par Sylviel » 05 Déc 2012, 17:54
Heu dans la formule rappelée ici il n'y a pas de v. Ici tu n'as pas une fraction mais tu as
exp(u) où
u = ...
et u' = ...
Alors la dérivée de exp(u) est (comme déjà rappelée) u'*exp(u)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
laureen
- Messages: 6
- Enregistré le: 05 Déc 2012, 13:08
-
 par laureen » 05 Déc 2012, 17:57
par laureen » 05 Déc 2012, 17:57
Sylviel a écrit:Heu dans la formule rappelée ici il n'y a pas de v. Ici tu n'as pas une fraction mais tu as
exp(u) où
u = ...
et u' = ...
Alors la dérivée de exp(u) est (comme déjà rappelée) u'*exp(u)
Donc sa ferait te^-t²/10000/5000 ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 05 Déc 2012, 18:00
par Sylviel » 05 Déc 2012, 18:00
Tu ne réponds pas aux questions dans l'ordre et tu ne mets pas de parenthèses... comment comprendre ce que tu écris ? :triste:
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
