Equations trigonométriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 21:27
par Maxime-59 » 30 Avr 2012, 21:27
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 30 Avr 2012, 21:30
par Kikoo <3 Bieber » 30 Avr 2012, 21:30
Maxime-59 a écrit:
De toute façon, j'ai dit que pour l'autre, c'était la même chose !

-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 30 Avr 2012, 21:40
par Maxime-59 » 30 Avr 2012, 21:40
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Mai 2012, 07:28
par Carpate » 01 Mai 2012, 07:28
C'est étrange !
Tu reconnais que les 2 solutions :

et
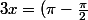 + 2 k\pi)
sont identiques et tu n'en tires pas la conclusion et continues d'écrire ;

et

Effectivement si tu n'avais pas réalisé que

tu ne risquais pas de voir que

En outre écrire (quand tu rédigeras)

n'est pas suffisant (d'ailleurs
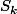
serait préférable à

)
k varie de 0 à 2


et il faut expliciter ces 3 valeurs sur ta copie.
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 11:10
par Maxime-59 » 01 Mai 2012, 11:10
Salut,
Merci pour ton aide de dernière minute!
Comment je dois faire pour exprimer avec les différentes valeurs de k ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 01 Mai 2012, 11:18
par Kikoo <3 Bieber » 01 Mai 2012, 11:18
Maxime-59 a écrit:Salut,
Merci pour ton aide de dernière minute!
Comment je dois faire pour exprimer avec les différentes valeurs de k ?
Bah tu fais "l'ensemble des solutions est :

ou

"
(Les deux écritures sont équivalentes !)
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 11:24
par Maxime-59 » 01 Mai 2012, 11:24
Ha c'est tout ? Je pensais qu'il fallait changer la réponse .. ^^
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 01 Mai 2012, 11:28
par Kikoo <3 Bieber » 01 Mai 2012, 11:28
Nan,
Ce que Carpate voulait te dire c'est que tu t'étais pas rendu compte que tes deux ensembles de solutions sont strictement les mêmes, donc il n'y avait pas besoin de créer deux ensembles pour rien... enfin chais pas si tu saisis ce que je veux dire, mais regarde,

, donc sois vigilant.
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 11:43
par Maxime-59 » 01 Mai 2012, 11:43
Oui, j'ai compris mais je ne savais pas qu'il fallait (dans ce cas) les mettre sous cette forme !
Merci pour votre aide, j'attaque de suite cette équation :
 -1 = 0)
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 11:48
par Maxime-59 » 01 Mai 2012, 11:48
Dans cet équation on sait que sin(0) = 0 rad. Il faut donc partir sur la piste de
 = cos(1))
?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Mai 2012, 11:50
par Carpate » 01 Mai 2012, 11:50
Maxime-59 a écrit:Oui, j'ai compris mais je ne savais pas qu'il fallait (dans ce cas) les mettre sous cette forme !
Merci pour votre aide, j'attaque de suite cette équation :
 -1 = 0)
OK
Indique-nous ta solution.
En tenant compte des remarques des nombreux intervenants ...
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 12:19
par Maxime-59 » 01 Mai 2012, 12:19
Tout bien réflechi, je pense plus qu'il faut faire comme cela :
-1 = 0)
=1)
=sin(\frac{\pi}{2})
C'est juste ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 01 Mai 2012, 12:21
par Kikoo <3 Bieber » 01 Mai 2012, 12:21
Maxime-59 a écrit:Tout bien réflechi, je pense plus qu'il faut faire comme cela :
-1 = 0)
=1)
=sin(\frac{\pi}{2})
C'est juste ?
Oui, pour l'instant c'est bon

Ne garde que le sinus, à gauche
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Mai 2012, 12:46
par Carpate » 01 Mai 2012, 12:46
Maxime-59 a écrit:Tout bien réflechi, je pense plus qu'il faut faire comme cela :
-1 = 0)
=1)
=sin(\frac{\pi}{2})
C'est juste ?
C'est juste mais tu pouvais aussi écrire :
 = \frac12 = sin(\frac{\pi}{6}))
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 14:23
par Maxime-59 » 01 Mai 2012, 14:23
Ha oui en effet, je n'aurai pas pensé à faire comme ça mais je t'avoue que le

m'embettait !
Comment je peux aboutir à la solution maintenant ?
+sin(\frac{\pi}{6}))
Franchement, je pense que c'est pas ça mais bon!
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Mai 2012, 14:31
par Carpate » 01 Mai 2012, 14:31
Maxime-59 a écrit:Ha oui en effet, je n'aurai pas pensé à faire comme ça mais je t'avoue que le

m'embettait !
Comment je peux aboutir à la solution maintenant ?
+sin(\frac{\pi}{6}))
Franchement, je pense que c'est pas ça mais bon!
Mais c'est exactement la même méthode que pour l'exercice précédent :
= sin(\frac{\pi}{6}))
a)

x = ... modulo
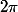
b)

x = ... modulo
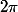
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 15:05
par Maxime-59 » 01 Mai 2012, 15:05
-
Maxime-59
- Membre Relatif
- Messages: 187
- Enregistré le: 26 Sep 2009, 23:25
-
 par Maxime-59 » 01 Mai 2012, 15:58
par Maxime-59 » 01 Mai 2012, 15:58
Ce n'est pas ça je présume ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 01 Mai 2012, 15:59
par Carpate » 01 Mai 2012, 15:59
Maxime-59 a écrit:
a)


.
b)


Remplacer les 3 points, c'est quand même élémentaire !
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 01 Mai 2012, 16:04
par Kikoo <3 Bieber » 01 Mai 2012, 16:04
Elémentaire, mon cher Watson !

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
et
m'embettait !
+sin(\frac{\pi}{6}))

