Équations

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:09

Bonjour, j'ai eu plusieurs équations à résoudre mais je bloque sur 2 !

=

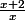
Et

Merci d'avance

par **Timothé Lefebvre** » 13 Sep 2009, 13:13

Salut :)

Dans la première, quelles sont les valeurs interdites ? Tu peux enlever les fractions après pour simplifier (en multipliant).

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:42

Les valeurs interdites sont 2 et 0.

En mutlipliant ?

par **Timothé Lefebvre** » 13 Sep 2009, 13:43

Oui, par exemple tu multiplies par x des deux côtés comme ça tu n'as plus de fraction à droite :)

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:45

On multiplie par nimporte quel nombre ?? ^o)

par **Timothé Lefebvre** » 13 Sep 2009, 13:46

Non :lol:

Par x :P

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:47

Hum c'est pas très clair dans mon esprit tout ça Hihi

par **Timothé Lefebvre** » 13 Sep 2009, 13:49

^^ Pourquoi ?! L'opération inverse de la division est bien la multiplication, pas vrai ? Donc si on veut enlever ce x au déno, on multiplie des deux côtés par x (en posant bien x différent de 0).

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:51

Donc on multiplierait par x=2 ?

par **Timothé Lefebvre** » 13 Sep 2009, 13:52

Non non ! Juste par x !

Ca donne :

Et après tu développes à gauche

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:55

Donc sa donne euh

par **Timothé Lefebvre** » 13 Sep 2009, 13:56

Non, quand on a un x comme ça on le multiplie juste au numérateur, ce qui donne ?

par **X_lOlly_pOp_X** » 13 Sep 2009, 13:57

Ce qui donne ...

par **Timothé Lefebvre** » 13 Sep 2009, 13:58

Tout à fait :)

Maintenant tu peux reproduire l'opération de ce côté.

Et sinon, on peut aussi remarquer qu'on a un produit en croix à faire ;) C'est même plus simple.

par **X_lOlly_pOp_X** » 13 Sep 2009, 14:02

un porduit en croix ? avec 2-x et x+2 ?

par **Timothé Lefebvre** » 13 Sep 2009, 14:05

En fait

=

revient à

Mea culpa, j'aurais du te dire de faire ça c'est plus simple. Sans oublier les deux valeurs de x à exclure car sinon les multiplications que l'on fait sont impossibles.

par **X_lOlly_pOp_X** » 13 Sep 2009, 14:09

Ok ok !!!! j"ai compris ça =D Enfin quelque chose que je comprend ... ^^
Mais après pour la résoudre on la dévellope ?

par **Timothé Lefebvre** » 13 Sep 2009, 14:10

Oui oui :D

Lol, c'est parce que ce que je disais au début était un peu tordu :P

Montre-moi ton développement, je corrige ;)

par **X_lOlly_pOp_X** » 13 Sep 2009, 14:12

Pas de soucis ^^

Hum Oula alors euh ça donnerai ...

(x+2)(2-x) = 3x²
2x-x²+4-2x = 3x²
-4x²+4=0

par **Timothé Lefebvre** » 13 Sep 2009, 14:12

Oui :)

Continue :)

Équations

Équations

Qui est en ligne