[Résolu] Equation avec x au cube

par **julien7200078** » 06 Sep 2010, 17:35

Bonjour,

Je suis devant une équation égal à 0 avec un x au cube. Je ne comprends pas comment résoudre cette dernière qui est:

x au cube-9x=0

Merci de m'aider.

par **Rebelle_** » 06 Sep 2010, 17:38

Bonjour ! :)

Tu peux peut-être factoriser ? ;)
Il y a déjà une solution très facile à trouver aussi...

=)

par **gigamesh** » 06 Sep 2010, 17:39

Bonjour,
commence par trouver un facteur commun aux deux termes du membre gauche ;
puis termine la factorisation avec une identité remarquable.

par **julien7200078** » 06 Sep 2010, 17:41

Je sais qu'il faut factoriser le problème est que je n'y arrive pas avec un x au cube. Merci de me donner le début car après la factorisation je connais la suite.

Merci de toutes vos réponses.

par **Rebelle_** » 06 Sep 2010, 17:43

D'accord.

x^3 - 9x = x(x^... - ...) = ...

par **julien7200078** » 06 Sep 2010, 17:46

Je ne vois pas du tout sur quel piste tu essaies de me mettre.

par **Dinozzo13** » 06 Sep 2010, 17:48

Salut !
Tu remarques que dans

tu as "

" comme facteur commun donc :

Or un produit est nul si et seulement si au moins l'un de ses facteur est nul :++:

par **gigamesh** » 06 Sep 2010, 17:49

Bah

c'est tout simplement

donc ça peut aussi s'écrire

par **Rebelle_** » 06 Sep 2010, 17:53

Dinozzo13 a écrit:Salut !
Tu remarques que dans tu as "" comme facteur commun donc :

Or un produit est nul si et seulement si au moins l'un de ses facteur est nul :++:

Coucou ! =)

Excuse-moi pour le hors-sujet, mais comment fais-tu pour écrire tes formules comme ça ?
Question peut-être bête mais bon :$

Merci

par **gigamesh** » 06 Sep 2010, 17:57

Rebelle_ a écrit:Coucou ! =)

Excuse-moi pour le hors-sujet, mais comment fais-tu pour écrire tes formules comme ça ?
Question peut-être bête mais bon :$

Merci

Un guide disponible sur le site :
http://maths-forum.com/showthread.php?t=70548

par **julien7200078** » 06 Sep 2010, 18:01

Pour la factorisation avec x(x²-9)=0 j'avais trouvé ça mais je pensais que c'était faux car après ca fait x=0 et x²=9 et cela ne peut pas être égal à x² mais à x ?

par **Rebelle_** » 06 Sep 2010, 18:04

Ah oui, je n'avais pas vu ça...
Merci bien :)

par **gigamesh** » 06 Sep 2010, 18:05

Ce n'est pas que c'est faux, c'est juste que tu n'as pas fini le travail...

Tu sais factoriser

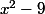
; une fois que c'est fait, tu vas t'apercevoir qu'il y a trois solutions en tout.

par **Rebelle_** » 06 Sep 2010, 18:05

julien7200078 a écrit:Pour la factorisation avec x(x²-9)=0 j'avais trouvé ça mais je pensais que c'était faux car après ca fait x=0 et x²=9 et cela ne peut pas être égal à x² mais à x ?

Si, c'est ça ! Et donc, la seconde équation a combien de solutions ? Quelles sont-elles ? (je t'aide là).

par **julien7200078** » 06 Sep 2010, 18:14

Je pense avoir trouvé cela ferait donc x=0 et (x-3)(x+3)=0 soit

x=0 ou x=3 ou x=-3

Cette équation a pour solution 0, 3 , -3 ?

par **Lostounet** » 06 Sep 2010, 18:17

Tout à fait!

par **Rebelle_** » 06 Sep 2010, 18:17

C'est bien ça =)

par **Olympus** » 06 Sep 2010, 18:20

julien7200078 a écrit:Je pense avoir trouvé cela ferait donc x=0 et (x-3)(x+3)=0

Correction : c'est un OU à la place du ET .

Sinon le reste est correct .

par **Rebelle_** » 06 Sep 2010, 18:23

Il avait corrigé juste en-dessous :P
Mais tu as raison de le signaler ^^

par **julien7200078** » 06 Sep 2010, 18:29

Oui j'ai pas fais gaffe en écrivant sur le net mais sur la feuille c'est bon :P Merci à tous pour votre aide. Bonne soirée.

[Résolu] Equation avec x au cube

[Résolu] Equation avec x au cube

Qui est en ligne